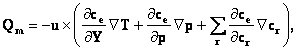2. Matematické základy geoinformatiky
Při řešení otázek spojených s projektováním, realizací a provozováním informačního systému je nutné převést konkrétní informační proces do abstraktní formy, která umožňuje:
- analyzovat strukturu a obsah informací;
- vytvořit zásady zápisu údajů, tj. rozhodnout o notaci čili způsobu tvorby záznamů;
- analyzovat a hodnotit informační proces s cílem jeho racionalizace (optimalizace) a automatizace;
- formulovat postupy výběru údajů z existující databáze;
- vytvořit postupy zpracování znalostí.
Protože se v současné a budoucí době budou realizovat komplexní vazebně náročné a interaktivní úlohy, které jsou obecně pro vědy o Zemi typické, je rozhodující systémová analýza problematiky jako základ projektování datové základny. Ta pak musí být utvořena tak, aby vypovídací schopnost shromažďovaných dat umožnila řešit všechny požadované úlohy.
Při analýze a řešení naznačených problémů se využívá řada matematických postupů z oboru:
- matematické logiky;
- teorie množin a fuzzy množin;
- teorie grafů; kombinatoriky;
- pravděpodobnosti;
- matematické statistiky.
V dalším textu jsou stručně připomenuty základy těchto disciplin a uvedeny oblasti jejich využití při řešení úkolů geoinformatiky a to nejen obecně, ale konkrétně v jednotlivých fázích informačního procesu.
2.1 Stavba matematických disciplín
2.1.1 Matematické disciplíny
Matematika jako věda je v nejširším pojetí členěna na základní disciplíny, algebru, geometrii, matematickou analýzu a aplikovanou matematiku.
Základními disciplinami jsou zde rozuměny formulace a analýza jazyka, axiomů a logických metod, na kterých je celá matematika založena (viz matematická logika). Teorie množin, jejímž zakladatelem byl Georg Cantor, nyní zakládá univerzální matematický jazyk.
Algebra historicky vznikla jako nástroj ke studiu řešení některých algebraických rovnic, zvláště polynomických funkcí jedné a více proměnných. Aritmetika a teorie čísel je část algebry, která se soustřeďuje na studium specielních vlastností čísel.
Geometrie se týká prostorové části matematiky, tj. vlastností a vztahů mezi body, přímkami, rovinami, obrazci, tělesy a povrchy těles. Topologie studuje strukturu geometrických objektů nejobecnějším způsobem.
Matematická analýza obsahuje jako svůj základ jednak diferenciální, jednak integrální počet. Zabývá se dále řešením diferenciálních rovnic, nekonečnými řadami atd.
Na rozdíl od předchozích čtyřech oblastí matematiky se aplikovaná matematika neustále rozrůstá o další obory významné v současných empirických vědách. Aplikovaná matematika zahrnuje dnes široké spektrum oborů starších i modernějších, jako např. teorii pravděpodobnosti, matematickou statistiku, matematickou fyziku, počítačové vědy (computer science). Zvláště díky rozvoji výpočetní techniky a jejího výpočetního potenciálu se mnohé z těchto oborů dále dělí. Příkladem může být matematická statistika; vedle klasické statistiky se rychle vyvinuly moderní statistické metody používané zvláště při popisu přírodních procesů (neparametrické statistiky a jiné).
2.1.2 Metody a nástroje
Jednou ze základních metod výstavby matematiky jako vědy je deduktivní metoda. Na základě přijatých předpokladů se odvozují důsledky z nich plynoucí. Neméně důležité jsou induktivní metody, tzn. procesy usuzující z jedinečných výroků na obecné závěry. Mezi oběma metodami nelze vést ostrou hranici, neboť obě metody jsou vnitřně spjaty.
Samotná výstavba matematiky se opírá o logiku a její výrokový kalkul. Výroky pak používá ve dvou pilířích matematiky: definicích a větách.
Definice je výrok (vyjádřený slovně nebo symbolicky), kterým se zavádí (definuje) nový pojem na základě pojmů již definovaných, a na základě vlastností a dokázaných vztahů mezi již definovanými pojmy.
Věta je - zhruba řečeno - vždy platný výrok (vyjádřený slovně nebo symbolicky). Větami se vyjadřují vlastnost definovaných pojmů. Velmi podstatné je, že věty je nutno dokázat. Ke každé uvedené větě se tedy váže její důkaz.
Důkaz je výrok nebo posloupnost výroků (nejčastěji implikací nebo ekvivalencí), jimiž se dokazuje platnost věty. Vytvoření důkazu je často jedním z nejobtížnějších kroků při výstavbě matematiky jako vědy. Důkazy se provádí pomocí předem stanovených pravidel odvozování (např. důkaz matematickou indukcí, přímý důkaz apod).
2.1.3 Axiomatická výstavba teorie
Matematika je tedy věda rozvíjející se zdola nahoru. Na základě již známých pojmů se větami dovozují jejich vlastnosti a vztahy mezi nimi, což umožňuje definovat další pojmy atd. Na druhé straně nějaký pojem X byl definován na základě již definovaných pojmů např. U a V. Pojem U však musel být definován na základě již definovaných pojmů např. A, B a C, obdobně pojem V. Pojem A musel však být definován na základě ... atd. Musí tedy existovat jakási soustava pojmů, které jsou ”úplně dole” (proces definic se nesmí zacyklit: nesmí být X definováno na základě U, U na základě A a A na základě X !).
Každá disciplína má svou soustavu základních pojmů, které se nedefinují, ale přijímají jako obecně známé. Takovým pojmem je např. v geometrii bod, v teorii množin množina a prvek množiny. Je samozřejmě žádoucí mnohé takové pojmy i popsat, nejen předpokládat jejich obecnou známost. Používá se proto tzv. pseudodefinice; nejčastěji výroku v běžném jazyce, který může obsahovat množství běžně užívaných podstatných a přídavných jmen (nikterak dále nedefinovaných), upřesňující pseudo - definovaný pojem.
Obdobně se to má se soustavou vět. Na základě dokázané platnosti jedné věty se dokazuje platnost jiné věty atd. Opačně tedy musí "dole" existovat věty, které jsou ”konečné”: pro ně už neexistují věty, na základě kterých by je bylo možno dokázat. Takové ”základní” věty se nazývají axiomy. Axiomy jsou výroky, které se přijímají bez důkazu jako zřejmá, evidentní, apriorně pravdivá tvrzení. Je zřejmé, že pro budování vědního oboru je žádoucí, aby systém axiomů byl co nejmenší. Na druhé straně je často možno vybudovat tutéž teorii na základě více (různých) systémů axiomů. Pro axiomatizaci vědních oborů se požaduje pouze to, že v odvozované teorii nesmí dojít ke sporu. Vůči takové interpretaci je pak výchozí axiomatický systém pravdivý. Na systém axiomů jsou obecně kladeny podmínky:
- nezávislosti: žádný z axiomů nelze odvodit z ostatních;
- úplnosti: přidání dalšího axiomu by vedlo ke sporu;
- bezespornosti: na základě axiomů nelze současně dovodit, že nějaká věta platí i neplatí současně.
- Libovolným bodem je možno vést přímku procházející libovolným jiným bodem.
- Každou přímku je možno libovolně prodloužit.
- Z libovolnému bodu je možno opsat kružnici s libovolným poloměrem.
- Všechny pravé úhly jsou si rovny.
- Jestliže přímka protínající dvě jiné přímky vytváří vnitřní úhly na stejné straně menší než dva pravé úhly, pak se tyto dvě přímky protnou na této straně.
- Každým bodem neležícím na přímce lze vést dvě rovnoběžky s přímkou
- Bodem neležícím na přímce nelze vést k přímce žádnou rovnoběžku
2.2 Teorie množin
Pojmy teorie množin a množinové operace se začaly stále častěji využívat (s rozvojem poznatků o možnostech využití metod různých matematických disciplín) při studiu geovědních objektů a jevů. Vyplývá to ze skutečnosti, že výsledkem řešení geovědních úloh je z formálního hlediska nalezení určité množiny objektů (bodů). Např. úlohu okonturování ložiskového tělesa si lze představit jako nalezení horní hranice podmnožiny bodů X![]() A, pro které platí, že x×d. Množinové vyjádření se široce využívá při tvorbě koncepčních modelů databází, např. v ER modelech (množina objektů a vztahů) nebo ERA modelech (množina objektů, vztahů a vlastností).
A, pro které platí, že x×d. Množinové vyjádření se široce využívá při tvorbě koncepčních modelů databází, např. v ER modelech (množina objektů a vztahů) nebo ERA modelech (množina objektů, vztahů a vlastností).
Za zakladatele teorie množin je považován Georg Cantor (1877). V dalším textu jsou uvedeny některé pojmy a pravidla, potřebná pro praktickou aplikaci teorie množin při řešení úloh geologické informatiky.
2.2.1 Základní pojmy
Kapitola předpokládá znalost základních pojmů teorie množin - samotného pojmu množina, prvek množiny, podmnožina, a také znalost základních množinových operací (sjednocení, průnik apod.). Zabývá se pouze pasážemi v těsné vazbě na geoinformatiku resp. informatiku obecně.
2.2.2 Kartézský součin
Kartézský součin množin A, B (značení: A×B) je množina všech uspořádaných dvojic takových, že první prvek dvojice je prvkem A a druhý prvek dvojice prvkem B:
Jsou-li množiny A a B konečné s počty prvků nA a nB, je i jejich kartézský součin A × B konečná množina; počet jejich prvků (= počet uspořádaných dvojic) je roven nA×nB - dvojice obsahují kombinace „každý z A s každým z B”. Pro grafické zobrazení kartézského součinu se pro množiny s malým počtem prvků může použít např. tabulka:

2.2.3 Relace
2.2.3.1. Pojem relace
Binární relace R z množiny A do množiny B
je libovolná podmnožina kartézského součinu A × B
![]() A × B
A × B![]() R, píšeme:
R, píšeme:
v množině A = {3, 5, 7, 9} je dána relace R = { [3,5], [3,7], [3,9], [5,7], [5,9], [7,9] }. Je tedy např. 3 R 7 nebo 7 R 9, ale 9 ¬ R 3
2.2.3.2. Vyjádření relací


Jsou-li množiny A a B konečné, lze pro znázornění relací použít několika způsobů. Nejčastěji používané jsou dva: maticový a tabulkový. Maticovým zápisem relace R z předchozího příkladu je následující matice vlevo 4×4 (nad matici resp. před matici byly pro přehlednost přidány nadpisy sloupců resp. řádků); v ní hodnota 0 značí, že prvky v relaci nejsou, hodnota 1 značí, že prvky v relaci jsou. Tabulkovým zápisem relace R je následující tabulka vpravo.
N-ární relace je libovolná podmnožina R kartézského součinu A1 × A2 × ... × An. Maticové zobrazení n-árních relací pro větší n je velmi nepraktické a nepřehledné. Proto se relace s konečným (často i značným) počtem prvků zobrazují výhradně jako n-sloupcové tabulky - pokud se samozřejmě nedají vyjádřit jinak, např. symboly výrokového počtu apod.
2.2.3.3. Relační databáze
Na shora zavedeném pojmu relace jsou konstruovány tzv. relační databáze. Nechť například množiny D, C a N značí po řadě množinu všech datumů, množinu všech textových řetězců (řetězec = posloupnost jednoho nebo více textových znaků) a množinu všech racionálních čísel. Mějme relaci R definovanou jako podmnožinu kartézského součinu

2.2.3.4 Vlastnosti relací
V následující tabulce jsou definovány některé základní typy relací podle svých vlastností; relace R je vždy v těchto případech relací v množině A:
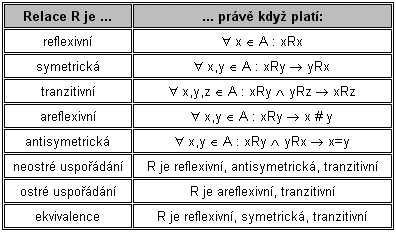
Nechť je dána relace - viz příklad odstavce ”Vyjádření relací”. Tato relace je areflexivní (pro všechna [x,y]
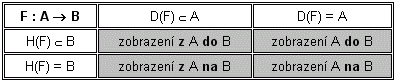
2.2.4 Zobrazení
F je zobrazení z A do B, právě když je F binární relace z A do B a současně platí:
Relace < z předchozího příkladu není zobrazení z A do A, protože je jednak 3<5 a jednak např. 3<7. Prvek 3 není v relaci s nejvýš jedním prvkem.
H(F) = { b | b
Na množině I přirozených čísel ( I = {1, 2, 3, ...} ) je dána relace ® takto: x→y
2.2.5 Operace
Nechť M1, M2,..., Mn, V jsou libovolné množiny. F
je n-ární operace z M1 × M2 ×
... × Mn do V,
je-li F (n+1)-ární relace, F
![]() M1 × M2 × ... × Mn
× V, a platí-li:
M1 × M2 × ... × Mn
× V, a platí-li:
Zobrazení definované v předchozím odstavci je unární operací ve smyslu definice n-ární operace. Obecně n-ární operace má n operandů. Specielně nulární operace nemá žádný operand; je pak z=F(), a protože z
Zobrazení ® z příkladu předchozího odstavce je tedy unární operací z I do I. Je-li y=®x, je y=x+1. Je proto ®3=4, ®28=29, ®(x+5)=x+6 pro x
2.2.6 Rozklad na třídy
Jedním z důležitých pojmů jak teorie množin, tak disciplín na ní stavějících, je pojem rozklad na třídy:
Systém S množin { A1, A2, ... , An } je disjunktním systémem, platí-li pro libovolné dvě množiny Ai, Aj
z S, že jejich průnik je prázdný: Ai
![]() Aj = {0}.
Aj = {0}.
Nechť je dána neprázdná množina P a neprázdný systém T = {
A1, A2, ... , An }, kde pro každé i je Ai
![]() P (T
je tedy systémem podmnožin množiny P). Tento systém T
nazýváme rozkladem množiny P na třídy, jestliže T
je disjunktním systémem a
P (T
je tedy systémem podmnožin množiny P). Tento systém T
nazýváme rozkladem množiny P na třídy, jestliže T
je disjunktním systémem a
![]() T=P. Každá Ai
T=P. Každá Ai
![]() T
se nazývá třída v T.
T
se nazývá třída v T.
Systém T je tedy rozkladem množiny P na třídy, jestliže průnik libovolných dvou tříd je prázdný a jejich sjednocením je celá množina P.
Jak bylo shora uvedeno, každé množině přísluší určující pravidlo, podle kterého byla množina vytvořena. Rozklad na třídy T je systémem podmnožin, je tedy sám množinou, existuje tedy i pro něj určující pravidlo. Velmi často mívá toto určující pravidlo matematickou podobu.
Barvy {červená, modrá, zelená, žlutá, jiná} rozkládají množinu všech jednobarevných aut na třídy. Tento rozklad B je tvořen pěti třídami (podmnožina červených aut, podmnožina modrých aut, ...). Sjednocení všech těchto tříd je celá množina všech jednobarevných aut, a každé dvě třídy jsou disjunktní (protože jde o jednobarevná auta, není žádné auto např. červené a zelené současně).
Věta: Každý rozklad množiny P na třídy definuje na P relaci ekvivalence. Každá ekvivalence na P definuje rozklad P na třídy.
2.2.7 Klasifikace
Při řešení otázek souvisejících s klasifikací dokumentů, sestavování tezaurů a formulování rešeršních hledisek je důležité najít optimální dělení množiny.
Definice: Klasifikací rozumíme roztřídění entit do skupin podle jejich podobnosti na základě společných vlastností. Dvě entity jsou ve stejné skupině, mají-li obě onu společnou vlastnost. Všechny entity tvoří dohromady výchozí množinu. Klasifikace tedy spočívá v nalezení vhodného rozkladu množiny na třídy.
Bibliografická klasifikace (třídění časopiseckých a sborníkových článků, knih, zpráv atd.) je založená na indexování, tj. přiřazení jednoho či více znaků k určité informační jednotce s cílem ji charakterizovat. Nejde tedy o pouhé roztřídění, ale o zobrazení obsahu dokumentu do redukované množiny znaků - číselných indexů, klíčových slov, deskriptorů. V pojmech teorie množin klasifikace množiny M je množina množin
- každý prvek x
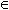 M náleží alespoň do jedné z množin Ai
množiny KM ;
M náleží alespoň do jedné z množin Ai
množiny KM ; - průnik množin Ai
 Aj = {0} , i ≠ j
Aj = {0} , i ≠ j - sjednocení množin A1
 A2
A2
 ...
...
 An = M
An = M
Klasifikační kritérium K pro množinu M znamená:
- zobrazení [ x
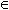 M → K(x) ] ,
M → K(x) ] , - že existují predikáty K1 ... Kn , tj. hodnoty klasifikačního kritéria.
Nechť M je klasifikovaná množina a K1 ... Kp jsou klasifikační kritéria s hodnotami 1K : 1K1 , 1K2 , .... , 1Ku (např. vědní obor), 2K : 2K1 , 2K2 , .... , 2Kv (např. autoři), 3K : 3K1 , 3K2 , .... , 3Kw (např. jazyky), Potom { M
2.2.8 Tezaurus
Definice: Nechť D = {D1, D2, ... , Dn} je množina dokumentů (knihovna) a nechť T = {T1, T2, . . , Tm} je množina klíčových slov (termínů), která v souhrnu postačí na charakterizování všech dokumentů. Pak množinu T spolu s množinou R vzájemných relací mezi termíny nazýváme tezaurus. Tabulka, která vyjadřuje, které prvky tezauru jsou přiřazeny k jednotlivým dokumentům, se nazývá dokument - termínová matice. margin-left:25px;
Dokumenty D jsou charakterizovány termíny T podle následujícího schématu:
D1: T1, T2, T3, T4
D2: T1, T3, T5
D3: T3, T5, T6, T7
D4: T2, T3, T6
D5: T1, T2, T4, T6
Tomu odpovídá následující dokument-termínová matice
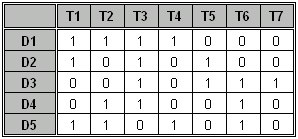
2.2.9 Teorie shlukování
Intuitivně chápeme, že dva objekty jsou si podobné, když mají některé vlastnosti shodné. Čím mají více shodných vlastností, tím jsou si podobnější. Z hlediska množinové teorie podobnosti můžeme objekt P1 charakterizovat jistou množinou vlastností {Vi} a objekt P2 množinou {Vj}. Vzájemnou podobnost lze určit pomocí koeficientu podobnosti
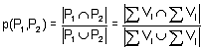
tj. podílu mohutnosti průniků a mohutnosti sjednocení množin. Podobně lze využít koeficient rozdílnosti d(P1,P2) = 1 - p(P1,P2)
Stanovme koeficient podobnosti objektů P1 = {V1, V2, V3, V4} a P2 = {V2, V4, V5} .
2.2.10 Fuzzy množiny
V souvislosti s potřebou řešit úlohy rozpoznávání obrazů se začala od počátku 60. let rozvíjet teorie fuzzy množin. V naprosté většině případů se setkáváme s problémem míry příslušnosti určitého objektu xi k jisté klasifikační třídě F. Přechod od jedné třídy k druhé není zpravidla skokový, ale spíše postupný. Otázka tedy není v tom, náleží-li objekt xi k třídě F, ale v tom, do jaké míry k ní náleží. Docházíme tak k závěru, že třída F obsahuje objekty xi s různou mírou ui příslušnosti k třídě
F = { m1|x1 , m2|x2 , ... , mn|xn},
V pojmech teorie množin lze interpretovat i JAZYK, který představuje souhrn dorozumívacích znaků a pravidel jejich používání a interpretace. Velmi důležitá jsou právě pravidla interpretace.
CUP ... české slovo v latince ... cup - cupitat, ... angl. slovo v latince ... kap - šálek, ... angl. slovo v azbuce ... sir - pán
Ke každé realitě (objektu) existuje pojem (obraz objektu). Jeho zobrazení množinou písmen je slovo. Množina slov pak tvoří jazyk. Pravidla, určující formu přiřazení, složení a pořadí prvků jazyka tvoří gramatiku. Přirozený jazyk je zobrazení množiny pojmů do množiny slov konkrétního jazyka.Vlastností a velkou předností všech jazyků je nejednoznačnost přiřazení (synonymie, homonymie), což ale přináší z hlediska informatiky značné komplikace.
V současné době je možné využitím počítačové techniky vytvářet jakékoliv klasifikace. Stejně tak využití teorie množin má velmi široké možnosti.
2.3 Matematická logika
Matematická logika má důležité místo v matematické lingvistice, v teorii vyhledávání a zpracování dotazů (tedy při zpracování vědeckých a průzkumných informací), v kybernetice, algoritmizaci a programování, ale také v konstrukci počítačů. V geovědách - např. geologických, se prakticky využívá při řešení řady problémů:
- při klasifikaci geologických objektů a jevů (například rudních a nerudních objektů);
- v úlohách analýzy vztahů mezi vlastnostmi různých skupin geologických objektů a jevů (např. mezi geologickou stavbou a lokalizací zrudnění);
- při řešení otázek prognózování;
- v rámci procesu zpracování geologických dat.
Protože matematická (formální) logika poskytuje základní nástroje pro popis výstavby ostatních věd obecně a informatiky zvláště, jsou v následujících odstavcích podány základy matematické logiky v potřebném rozsahu.
2.3.1 Binární algebra
Historicky nejstaršími hodnotami v logice jsou pravda a nepravda. Na základě těchto hodnot vznikla jako nejpropracovanější dvouhodnotová (binární) logika. Její matematické základy podal George Bool, který zveřejnil základní práce v roce 1847 a 1854. Proto se algebra vybudovaná nad dvěma různými hodnotami nazývá také Booleova algebra. Binární logika a binární algebra jsou základem číslicových počítačů. Jejich konstrukce se opírá zásadně o dvě hodnoty, ač modelovanými různými fyzikálními principy: zmagnetováno - nezmagnetováno; pod napětím - bez napětí; vede - nevede; odráží - neodráží atd.
2.3.1.1 Logické hodnoty
Různé principy vyjádření dvou stavů (nejen fyzikálních) modeluje binární algebra dvěmi hodnotami a vyjadřuje dvěma symboly:
1 - platí (často také symbol písmene I).
2.3.1.2 Logické proměnné
Stejně jako v jiných oborech matematiky označujeme symbolicky ty objekty, které mohou nabývat různých hodnot. Zavádíme tak logické proměnné. Uvedeme-li například, že X je logická proměnná, pak to znamená, že X může nabývat (logických) hodnot 0 nebo 1.
2.3.1.3 Logické operace
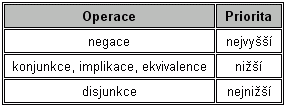
Nad logickými hodnotami 0 a 1 (které mohou být reprezentovány logickými proměnnými) jsou zavedeny logické operace. Operace nad binárními hodnotami se nejčastěji popisují pomocí tzv. pravdivostní tabulky: Nejpoužívanější operace popisuje následující souhrnná tabulka:
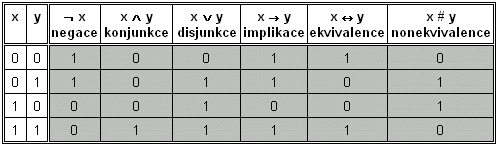
ve formálních jazycích se často místo znaménka ¬ používá tří písmen "not" zapsaných bezprostředně (bez mezer) za sebou a chápaných jako jeden nedělitelný symbol. Obdobně místo znaménka
2.3.1.4 Logické výrazy
2.3.1.4.1 Výrazy a priority
Logické výrazy se tvoří stejně jako výrazy např. aritmetické. Zápis logického výrazu tvoří buď jediná logická hodnota (kterou může reprezentovat logická proměnná), zápis logické operace (unární nebo binární), nebo logický výraz uzavřený do závorek ( ). Ve druhém případě jsou operandem nebo operandy logické výrazy, tj. buď logické hodnoty, nebo logické operace, nebo logické výrazy uzavřené do závorek ... atd.
Takto definovaný výraz je definován tzv. rekurzivně: ke své vlastní definici používá sám sebe. Takové definice jsou podstatnou součástí definic např. v teorii automatů a gramatik.
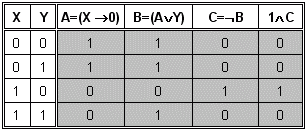
2.3.1.4.2 Vyhodnocování výrazů s proměnnými
Nejpohodlněji, s nejmenšími chybami, lze vyhodnotit výraz obsahující proměnné pomocí pravdivostní tabulky. Na příklad shora uvedený výraz
2.3.2 Abecedy a jazyky
2.3.2.1 Abecedy a slova
Abeceda je konečná množina prvků. Symbol je libovolný prvek abecedy. Dvě abecedy jsou disjunktní, jsou-li to dvě disjunktní množiny.
Latinka = {A, B, C, ..., X, Y, Z} Kamenika = {mezera, a, á, b, c, č, ..., z, ž, A, Á, ..., Ž} Abeceda dekadických číslic = {0, 1, 2, …, 8, 9} Abeceda římských číslic = {M, D, C, L, X, V, I}
Nechť S = (p1 p2 .. pn), pi
![]() A, je neprázdné slovo v abecedě
A. Označme X = (p1 p2 .. pi-1), Y = (pi pi+1 ... pj-1 pj), Z = (pj+1 ... pn-1 pn).
X, Y
i Z jsou tedy také
slova v abecedě A, alespoň jedno z nich neprázdné. Nechť Y je neprázdné slovo. Pak
definujeme: X je prefixem slova Y
ve slově S, Z je postfixem
slova
Y ve slově S. Každé ze slov X,
Y, Z jsou podslova
slova
S.
Prázdné slovo je podslovem každého slova. Každé slovo má prázdný prefix a prázdný postfix. Dvě slova jsou stejná, jsou-li to stejné posloupnosti symbolů dané abecedy (tj. zvláště co do počtu a co do pořadí). Dvě slova jsou různá, nejsou-li stejná.
A, je neprázdné slovo v abecedě
A. Označme X = (p1 p2 .. pi-1), Y = (pi pi+1 ... pj-1 pj), Z = (pj+1 ... pn-1 pn).
X, Y
i Z jsou tedy také
slova v abecedě A, alespoň jedno z nich neprázdné. Nechť Y je neprázdné slovo. Pak
definujeme: X je prefixem slova Y
ve slově S, Z je postfixem
slova
Y ve slově S. Každé ze slov X,
Y, Z jsou podslova
slova
S.
Prázdné slovo je podslovem každého slova. Každé slovo má prázdný prefix a prázdný postfix. Dvě slova jsou stejná, jsou-li to stejné posloupnosti symbolů dané abecedy (tj. zvláště co do počtu a co do pořadí). Dvě slova jsou různá, nejsou-li stejná.
Ačkoliv se zdá, že rovnost slov je naprosto jasná, zavádějí některé informační systémy rovnost odlišně; např. tak, že dvě slova jsou stejná, je-li jedno z nich prefixem druhého. To má dobrý smysl při vyhledávání podle kriterií. Vyhledat všechny informace, kde příjmení = NOV znamená pak vyhledat nejen příjmení NOVÝ, ale i NOVÁK, NOVOTNÁ atd.
2.3.2.2 Jazyky
Nechť je dána abeceda A. Množinu všech jejich slov označme A* (Pozn.: množina A* je nekonečná!). Označme LA libovolnou podmnožinu množiny A* (množina LA může být i množinou A*). Pak definujeme: Formální jazyk (často také jen jazyk) nad abecedou A je uspořádaná dvojice [A, LA]. Je-li množina LA konečná, nazývá se jazyk L konečný; je-li prázdná, nazývá se jazyk L prázdný; je-li nekonečná, nazývá se jazyk L nekonečný.
Čeština je konečný jazyk nad Kamenikou (ve smyslu zavedení abecedy Kamenika shora).
2.3.2.3 Automat
Automat je procedurální systém, který po předložení slova konečným počtem kroků rozpozná, zda se jedná nebo nejedná o slovo dané abecedy.
2.3.2.4 Gramatika
Gramatika je generativní systém, který opakovaným užitím vytváří postupně všechna slova pouze daného jazyka.
Formálními jazyky a gramatikami se zabývá poměrně nová, v informatice však velmi významná oblast aplikované matematiky, teorie automatů.
2.3.3 Výroky a výrokové formy
2.3.3.1 Výrok
Základním objektem logiky je výrok. Logika pak zkoumá jeho obsahové a pravdivostní hodnoty a pravidla seskupování výroků. Jde o základní pojem; proto se výrok nedefinuje, pouze se popíše, co se pojmem rozumí. Nejčastěji se výrok definuje takto: výrok je tvrzení, o jehož pravdivosti má smysl uvažovat nebo také výrok je napsaná nebo vyslovená myšlenka, o jejíž pravdivosti má smysl uvažovat.
"Tato hornina je granit."
(x + 1)2 = x2 + 2x + 1
Důležitým faktorem v definici výroku je to, že o pravdivosti má smysl uvažovat. Aby výrok byl výrokem, nemusí být jeho pravdivostní hodnota známa právě teď, dokonce ani nemusí být zřejmé, jakým způsobem by se pravdivostní hodnota určila. Výrok, o jehož pravdivosti nejsme schopni rozhodnout, se nazývá hypotéza.
To, zda výrok je či není hypotézou, je převážně subjektivním hodnocením. Cílem zkoušky na vysoké škole je ověřit, zda jednoznačně pravdivé nebo nepravdivé (z hlediska pedagoga) výroky, kterými studenti prezentují své znalosti, nejsou (z hlediska studenta) pouhými hypotézami.
2.3.3.2 Abeceda výrokového jazyka
Abecedou je množina písmen, číslic a specielních symbolů používaných v té které disciplíně (např. symbol =). Zápis výroků je pak většinou jednodušší než zápis běžnou větou. Ovšem při čtení výroků zapsaných za pomocí specielních symbolů se vlastně provádí substituce symbolů jedním nebo více slovy běžného jazyka (např. A=B čteme "á je rovno bé"). Proto se specielní symboly tvořící abecedu často považují za metasymboly; každý takový metasymbol je pak při zpracování substituován jedním nebo více slovy, které už metasymboly neobsahují.
2.3.3.3 Kvantifikátory
Pro zápis výroků se v matematických disciplínách (kromě mnoha dalších specielních symbolů) používají kvantifikátory.
2.3.3.3.1 Existenční kvantifikátor
Existenční kvantifikátor
![]() slouží k zápisu takového výroku, který sděluje, že existuje alespoň jeden objekt
(prvek nějaké množiny) mající nějakou vlastnost.
slouží k zápisu takového výroku, který sděluje, že existuje alespoň jeden objekt
(prvek nějaké množiny) mající nějakou vlastnost.
2.3.3.3.2 Všeobecný kvantifikátor
Všeobecný kvantifikátor
![]() slouží k zápisu takového výroku, který sděluje, že všechny objekty (prvky nějaké
množiny) mají nějakou vlastnost.
slouží k zápisu takového výroku, který sděluje, že všechny objekty (prvky nějaké
množiny) mají nějakou vlastnost.
2.3.3.4 Výroková forma, výroková proměnná
Výrokem je příklad shora: „Tato hornina je granit”. Ukážeme-li na nějakou horninu a proneseme uvedenou větu, pak jistě někdo může rozhodnout, zda to je či není pravda. Ukážeme-li na jinou horninu a opět proneseme uvedenou větu, opět jde o výrok. Jestliže se však snažíme generalizovat a vytvoříme konstrukci X je granit pak nejde o výrok; nelze rozhodnout o pravdivosti nebo nepravdivosti, protože není konkrétně řečeno, co to X je. Výrokem se uvedená konstrukce může stát po ”dosazení za X”. Takové konstrukce se nazývají výrokové formy a symboly (zde např. X), za které se dosazuje, se nazývají výrokové proměnné.
Výroková forma V(X) je výraz, který se skládá ze slov, symbolů a z výrokových proměnných. Dosazením konkrétních hodnot za výrokové proměnné vznikne výrok.
Výroková forma V může mít více výrokových proměnných: V = V (X, ... , Z). Pokud nebude řečeno v dalším textu jinak, bude sice užíváno zápisu V (X), ale pod X bude myšlen seznam výrokových proměnných: posloupnost jedné nebo více výrokových proměnných oddělených čárkou.
výroková forma V (x,y): y = x2 výrok (pravdivý) dosazením 4 za y, 2 za x: 4 = 22 výrok (nepravdivý) dosazením 6 za y, 3 za x: 6 = 32
2.3.3.4.1 Definiční obor výrokové formy
Pokračujme v předchozím příkladu: dosazením poněvadž za y, 8 za x dostaneme poněvadž = 82 což není výrok. Dosadit za výrokovou proměnnou (aby se výroková forma stala výrokem) není tedy možno cokoliv. Definičním oborem D (V) výrokové formy V(X) je množina všech takových A, pro něž je V(A) výrokem.
Forma "X je sudé" má za definiční obor "Množinu celých čísel Z". Forma "X má porfyroblastickou texturu" má smysl pro obor "Metamorfované horniny".
2.3.3.4.2 Obor pravdivosti výrokové formy
Pro některá A
![]() D (V) je výrok V (A) pravdivý, pro některá ne (vždy ovšem V (A) je výrokem).
Definice: Podmnožina
P (V)
D (V) je výrok V (A) pravdivý, pro některá ne (vždy ovšem V (A) je výrokem).
Definice: Podmnožina
P (V)
![]() D(V) všech takových A
D(V) všech takových A
![]() D (V), pro něž
je V(A) pravdivým
výrokem, se nazývá obor pravdivosti výrokové formy V(X).
D (V), pro něž
je V(A) pravdivým
výrokem, se nazývá obor pravdivosti výrokové formy V(X).
Obor pravdivosti pro formu V (X): "X je sudé" je množina sudých čísel P(V) = {X
2.3.3.4.3 Tautologie
Definice: Tautologie je výroková forma V(X), jejíž obor pravdivosti je roven jejímu definičnímu oboru:
2.3.3.5 Operace s výroky, složené výroky
Výrok může nabývat hodnoty pravda a nepravda. Z tohoto hlediska na něj můžeme pohlížet jako na jedno z vyjádření hodnoty binární algebry. Proto se na něj vztahuje vše to, co bylo řečeno v kapitole shora.
Označíme-li jeden výrok A a druhý B, lze z nich především konstruovat logické výrazy pomocí logických operací. Zkoumáme pak, jak se to má s platností B → A apod. Výsledkem může být opět jen platnost nebo neplatnost. Protože lze rozhodnout, zda B → A platí nebo ne, je B → A výrokem. Takový výrok nazýváme složeným výrokem.

Jestliže číslo končí nulou, pak je dělitelné dvěma. Pravdivostní tabulka je uvedena výše. Z tabulky je vidět, že uvedený složený výrok je pravdivý kromě případu, že číslo je sice dělitelné dvěma, ale nekončí nulou.
Podle rešeršního požadavku chceme vybrat dokumenty, které: popisují problémy, vyjádřené deskriptory A (Český masiv), B (zlomová tektonika), C (ložiska Pb-Zn) a D (mineralogie) nebo deskriptory A (Český masiv) a C (ložiska Pb-Zn); jsou z roku 1984 nebo 1985; jsou psány cizím jazykem, tj. nejsou české (ČJ) a slovenské (SJ). Zápis požadavku pro vyhledávání je pak výrazem ( A and B and C and D) or (A and C)) and (1984 or 1985) and (ČJ or SJ) ) Při procházení (např. databáze dokumentů) se pak tento výraz vyhodnocuje pro každý dokument a do výběru budou zahrnuty pouze ty, pro něž je výsledná hodnota pravda. Poznamenejme, že většina starších databází (založených před rokem 1980) měla pouze tři možnosti operací s výroky, a to konjunkci, disjunkci a negaci. Ostatní operace bylo nutno vyjadřovat výrazy pomocí konjunkce, disjunkce a negace.
2.3.3.6 Poznámky k logickým výrazům
Při praktickém využívání matematické logiky (a obecně všech metod klasické matematiky) narážíme na rozpor mezi přesností matematického popisu a složitostí popisované skutečnosti. Bertrand Russel (1923) napsal, že "tradiční logika předpokládá použití přesných pojmů, které jsou však aplikovatelné pouze v ideální představě". Snaha o stále větší přesnost vede k neúměrnému nárůstu definic a rozsahu popisu prakticky zcela jednoduchých jevů (Novák, 1990). Zvláště komplikovaná situace nastává při práci s přirozeným jazykem, který vyniká mnohotvárností a schopností pracovat s vágními, tj. nepřesně určenými pojmy, které vymezují určitou třídu objektů bez jasných hranic.
antický paradox hromady (sorites) „Ubírejme z hromady kamení jeden kámen po druhém. Ve kterém okamžiku přestane existovat hromada a zůstane jen pár kamenů?”
antický paradox holohlavého člověka (falakros): „Jestliže holohlavému člověku naroste jeden vlas navíc, zůstává holohlavý. Naroste-li mu však např. 80 000 vlasů, je ještě holohlavý?” Samozřejmá odpověď zní „ne”, logicky však vyplývá, že „ano”. Paradox totiž ve správné formulaci zní: On ... "člověk mající n vlasů je holohlavý" a tedy jde o množinu speciálních axiomů
2.3.4 Fuzzy logika
Pod pojem fuzzy logika se zahrnují logiky obecnější povahy a to vícehodnotová logika a lingvistická logika.
2.3.4.1 Vícehodnotová logika
je logika s více než dvěma pravděpodobnostními hodnotami zpravidla z intervalu <0,1>. Je přímým zobecněním klasické dvouhodnotové logiky. Polský matematik J. Lukasiewicz nejprve vybudoval tříhodnotovou logiku s pravdivostními hodnotami [ANO, NEVÍM , NE] a později ji rozšířil na logiku se spočetně mnoho pravdivostními hodnotami.
Obdobně jako klasická logika pracuje i vícehodnotová logika s výroky spojovanými pomocí spojek (disjunkce, konjunkce, odvážná konjunkce, implikace, intenzifikátory atd.) do složených výroků.
existuje-li mezi spojovanými výroky jisté vnitřní (kontextuální) ovlivnění, jde o odvážnou konjunkci.
Mějme výroky "Jan je tlustý" a "Jan je podobný Petrovi": "tloušťka" je součástí "podoby" a proto je konjunkce "Jan je tlustý a podobný Petrovi" odvážná (pravdivost složeného výroku je menší než pravdivost každého z obou výroků).
2.3.4.2 Lingvistická logika
je mnohem radikálnějším zobecněním klasické dvouhodnotové logiky. Vychází z předpokladu, že lidskému uvažování je přirozené vyjadřovat pravdivostní hodnoty lingvisticky, např. pomocí slov [PRAVDA, VÍCEMÉNĚ PRAVDA, ČÁSTEČNÁ PRAVDA, ČÁSTEČNÁ NEPRAVDA, NEPRAVDA, NEZNÁMO]. Významy těchto slov jsou hodnotami fuzzy množiny, která nemusí být uzavřená. Jejich pravdivostní hodnota je vyjadřována pomocí určitého pravidla v intervalu <0,1>.
Porovnání kyzového polymetalického ložiska Zlaté Hory s typy vulkanogenních sulfidických ložisek Kuroko, Rosebery, Besshi a Kypr na základě fuzzy lingvistické diagnostiky (Patočka-Vrba, 1989) ukazuje na jistou se příbuznost k typu Rosebery, ale podle primárních rysů je vyšší k typu Kuroko a podle druhotných (spjatých s regionální metamorfózou) k typu Besshi (viz tab. 2.1).
Tab. 2.1: Příbuznost ložiska Zlaté Hory s typy vulkanogenních ložisek (Patočka-Vrba, 1989)
| diagnostický standard | primární rysy | sekundární rysy | celkový soubor |
| typ Kuroko | 1 | 0 | 0 |
| typ Rosebery | 1 | 1 | 1 |
| typ Besshi | 0 | 1 | 1 |
| typ Kypr | 0 | 0 | 0 |
2.3.5 Logické metody v geovědách
Logické metody (označované také jako logicko-informační, logicko-kombinatorní, logicko-matematické) jsou v geovědách vědách používány pro řešení:
- úloh geologické informatiky
- problémů prognózování perspektivních objektů v zájmových oblastech
- analýzy logických závislostí mezi objekty a jevy
- posuzování podobnosti objektů atd.
Svou podstatou jde o heuristické procedury, založené buď zcela nebo částečně na postupech matematické logiky.
2.4 Kombinatorika
Kombinatorika je nauka o možnostech kombinování, tj. přeskupování prvků. Představuje velmi staré odvětví matematických věd. Z hlediska geologické informatiky je využívána při řešení pravděpodobnostních úloh v oblasti vědeckých informací, při automatickém zpracování textů apod. V této kapitole uvádíme jen zcela nejzákladnější pojmy.
Permutace z n prvků je každá uspořádaná n-tice utvořená z daných n různých prvků. Počet permutací z n prvků je P(n) = n!
Utvořme permutace z množiny M {a, b, c}.
Počet permutací je P(3) = 3! = 3 x 2 x 1 = 6.
Vzniklé skupiny jsou: abc, acb, cab, bac, bca, cba
Kolik dvoupísmenových a trojpísmenových slov lze utvořit z 10 různých písmen?
10! = 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1
(10-2)! = 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1
(10-3)! = 7 x 6 x 5 x 4 x 3 x 2 x 1
V2(10) = 10! / (10-2)! = 10 x 9 = 90
V3(10) = 10! / (10-3)! = 10 x 9 x 8 = 720
Kombinace k-té třídy z n různých prvků jsou skupiny, z nichž každá obsahuje k prvků z daných n prvků, přičemž na pořadí prvků ve skupině nezáleží. Počet kombinací je
(n nad k) je tzv. kombinační číslo.
Kombinace se prakticky využívají při úvahách o možném počtu rejstříků v bibliografii. Nejčastěji se používají 2 - 3 rejstříky (autorský, přírůstkový a předmětový). Ke každé knize se vztahuje okolo 20 základních údajů (aspektů, klasifikačních hledisek) a to - přírůstkové číslo, vědní obor, MDT, autor, instituce, redaktor (překladatel), pracoviště redaktora, titul knihy, titul v originále, vydavatelství, jazyk, země vydání, způsob získání, počet stran, počet obrázků, rok vydání, cena atd. Při 20 třídících aspektech lze teoreticky vytvořit:
20! / 1!(20-1)! = 20 jednoaspektových rejstříků
20! / 2!(20-2)! = 190 dvojaspektových rejstříků
20! / 3!(20-3)! = 1140 trojaspektových rejstříků
20! / 4!(20-4)! = 4845 čtyřaspektových rejstříků
Kombinace s opakováním k-té třídy z n prvků jsou skupiny po k prvcích z daných n prvků, přičemž každý prvek se ve skupině může vyskytnout až k-krát. Počet kombinací s opakováním je
2.5 Teorie grafů
Teorie grafů se využívá při řešení nejrůznějších úloh v řadě geovědních disciplin (v geologii např. popis vývoje geologických procesů, optimalizace průzkumných procesů, stromové grafy klasifikací apod.). Nespornou předností postupů, vycházejících z této teorie, je názornost.
Síťový graf (síťový model, logická síť) je názorné zobrazení procesu (projektu) ve tvaru grafu, který vyjadřuje vazby (logické, technologické) mezi dílčími ději (činnostmi).
2.5.1 Základní pojmy teorie grafů
V této kapitole jsou definicemi zavedeny grafy a jejich komponenty, a jsou podány jejich základní vlastnosti a vztahy. Kapitola sice v následujícím odstavci definuje grafy tak, jak je to v matematice obvyklé - zcela abstraktně, poté však přesnost výkladu omezuje na podporu názornosti.
2.5.1.1 Definice grafu
Mějme konečnou množinu V; její prvky nazývejme vrcholy nebo také uzly; množina V je tedy množina vrcholů nebo také množina uzlů. Mějme konečnou množinu E; její prvky nazývejme hrany. Množina E je tedy množina hran. Označme ve shodě s předchozími kapitolami
V2 = V * V = { {u,v} | u
Pro lepší pochopení uveďme nyní obrázek 2.1 (zřejmě nejnázornější a také nejpoužívanější vizualizaci grafu) a na něm objasněme podanou definici.

Obr. 2.1: Příklad grafu
Je až s podivem, že něco tak zřejmého, jako je na obrázku 2.1, může mít tak nepochopitelnou definici. Ta má však své důvody - teorie grafů totiž vznikla na základě potřeby zobecnit a formalizovat právě taková schémata, jako jsou na obrázku. Může jít např. o schémata dopravních cest, závislosti činností, rozvod energií apod. Právě z tohoto "zpětného" aspektu se podívejme na definici grafu.
Především máme uzly, z nichž některé jsou propojené (některé jednosměrně). To je tedy množina V uzlů zde znázorněna kruhy se symboly 1 až 5. Úsečky a až g, z nichž některé mají koncovou šipku, pak tvoří jinou množinu - v definici označenou jako množina E hran.
Pro hrany je však typické, že vždy "spojují" dva uzly, každá hrana právě dva uzly. Pro popis, které dva uzly spojuje která hrana, je zavedena především množina uspořádaných dvojic (kartézský součin V×V, v definici označený V2). Prvkem tohoto součinu je např. dvojice [1,2] a také dvojice [1,3] (obojí v tomto pořadí!). Uzly 1 a 5 spojeny nejsou, uzly 1 a 3 však ano - úsečkou c s naznačenou orientací: vychází z 1 a končí v 3. Lze tedy říci, že hrana c inciduje s vrcholy 1 a 3 (v tomto pořadí), obdobně hrana e s vrcholy 3 a 4 (opět v tomto pořadí). To však odpovídá tomu, že je definováno zobrazení z množiny hran do množiny uspořádaných dvojic vrcholů a protože záleží na pořadí vrcholů, má smysl mluvit o orientaci: hrana je orientována z jednoho vrcholu (počátečního) do jiného (koncového). V případě např. silniční sítě může jít o jednosměrné ulice.
Na druhé straně u jiné hrany (např. b) orientace naznačena není. Jistě např. v silniční síti lze některými ulicemi projet tam i zpět. Nelze tedy jeden vrchol nazvat počátečním a jiný koncovým. Proto byla zavedena množina dvouprvkových množin vrcholů - v definici označena V2. Hrana b pak inciduje nikoliv s uspořádanou dvojicí [1,2], ale s dvouprvkovou množinou, která je evidentně rovna množině {1,2}. To však odpovídá tomu, že je definováno zobrazení z množiny hran do množiny dvouprvkových množin vrcholů. Protože nemá smysl používat termíny počáteční a koncový, zavádí se zde pojem krajní uzly hrany.
Pro jednotnou definici incidence hran s vrcholy je proto požadováno zobrazení do množiny sjednocující jak uspořádané dvojice vrcholů, tak ("neuspořádané") dvouprvkové množiny vrcholů - a to je množina J z definice.
2.5.1.2 Hrany, uzly
Teorie grafů dále definuje řadu pojmů používaných pro popis vlastností grafů. Bez nároku na exaktnost uveďme některé z nich - často mají pojmy zcela názorný význam:
V obecném grafu může zobrazení incidence F přiřazovat dvěma nebo více různým hranám stejnou dvojici vrcholů (uzlů). Zobrazení tedy nemusí být prosté. Různé hrany, které jsou zobrazeny na stejnou dvojici vrcholů (uzlů), se nazývají rovnoběžné (paralelní) hrany. Množinu všech e
![]() E
takových, že F(e)
E
takových, že F(e)
![]() V2 nazýváme množinou neorientovaných hran
grafu G a její prvky neorientované hrany. Množinu všech e
V2 nazýváme množinou neorientovaných hran
grafu G a její prvky neorientované hrany. Množinu všech e
![]() E takových, že F(e)
E takových, že F(e)
![]() V2 nazýváme množinou orientovaných hran grafu G a její prvky orientované hrany. Množinu
všech e
V2 nazýváme množinou orientovaných hran grafu G a její prvky orientované hrany. Množinu
všech e
![]() E takových, že F(e)
E takových, že F(e)
![]() { {v,v} | v
{ {v,v} | v
![]() V }
nazýváme množinou neorientovaných smyček grafu G
a její prvky neorientované smyčky. Množinu všech e
V }
nazýváme množinou neorientovaných smyček grafu G
a její prvky neorientované smyčky. Množinu všech e
![]() E takových,
že F(e)
E takových,
že F(e)
![]() { [v,v] | v V } nazýváme množinou orientovaných smyček
grafu G a její prvky orientované smyčky. Pokud
množina E obsahuje pouze neorientované hrany a neorientované smyčky,
nazývá se graf G neorientovaný graf. Pokud množina
E obsahuje pouze orientované hrany a orientované smyčky, nazývá
se graf G orientovaný graf.
{ [v,v] | v V } nazýváme množinou orientovaných smyček
grafu G a její prvky orientované smyčky. Pokud
množina E obsahuje pouze neorientované hrany a neorientované smyčky,
nazývá se graf G neorientovaný graf. Pokud množina
E obsahuje pouze orientované hrany a orientované smyčky, nazývá
se graf G orientovaný graf.
Buď e
![]() E orientovaná hrana. Je tedy F(e)=[u,v]
E orientovaná hrana. Je tedy F(e)=[u,v]
![]() V2.
Vrchol (uzel) u nazýváme bezprostředním předchůdcem
(také rodičem) vrcholu (uzlu) v. Vrchol (uzel) v nazýváme bezprostředním následníkem (také potomkem) vrcholu (uzlu) u. Krajní vrcholy (uzly) neorientované smyčky jsou totožné. Počáteční a koncový vrchol (uzel) orientované smyčky jsou totožné. Počet hran, jimž je vrchol (uzel)
v neorientovaného grafu G krajním vrcholem, se nazývá stupněm vrcholu (uzlu)
v. Počet hran, jimž je vrchol (uzel)
v orientovaného grafu G počátečním vrcholem,
se nazývá výstupním stupněm vrcholu (uzlu)
v. Počet hran, jimž je vrchol (uzel) v orientovaného grafu G
koncovým vrcholem, se nazývá vstupním stupněm vrcholu (uzlu)
v.
V2.
Vrchol (uzel) u nazýváme bezprostředním předchůdcem
(také rodičem) vrcholu (uzlu) v. Vrchol (uzel) v nazýváme bezprostředním následníkem (také potomkem) vrcholu (uzlu) u. Krajní vrcholy (uzly) neorientované smyčky jsou totožné. Počáteční a koncový vrchol (uzel) orientované smyčky jsou totožné. Počet hran, jimž je vrchol (uzel)
v neorientovaného grafu G krajním vrcholem, se nazývá stupněm vrcholu (uzlu)
v. Počet hran, jimž je vrchol (uzel)
v orientovaného grafu G počátečním vrcholem,
se nazývá výstupním stupněm vrcholu (uzlu)
v. Počet hran, jimž je vrchol (uzel) v orientovaného grafu G
koncovým vrcholem, se nazývá vstupním stupněm vrcholu (uzlu)
v.
2.5.1.3 Sledy, vzdálenosti, souvislost
Nechť G = {V, E, F} je neorientovaný graf. Nechť v0, v1, ...
, vn-1, vn jsou vrcholy (uzly) z V. Nechť h1, h2,
... , hn jsou hrany z E takové, že F(hi) = {vi-1,vi}
pro všechna i
![]() <1,n>. Pak posloupnost s=[v0, h1, v1, ... ,
hn, vn] se nazývá (neorientovaným) sledem mezi vrcholy (uzly) v0 a vn. Říkáme také, že v0 a vn jsou dostupné, nebo že
v0 (vn) je dostupný z vn (v0).
Nechť G = {V, E, F} je orientovaný graf. Nechť v0, v1, ...
, vn-1, vn jsou vrcholy (uzly) z V. Nechť h1, h2,
... , hn jsou hrany z E takové, že F(hi) = {vi-1,vi}
pro všechna i
<1,n>. Pak posloupnost s=[v0, h1, v1, ... ,
hn, vn] se nazývá (neorientovaným) sledem mezi vrcholy (uzly) v0 a vn. Říkáme také, že v0 a vn jsou dostupné, nebo že
v0 (vn) je dostupný z vn (v0).
Nechť G = {V, E, F} je orientovaný graf. Nechť v0, v1, ...
, vn-1, vn jsou vrcholy (uzly) z V. Nechť h1, h2,
... , hn jsou hrany z E takové, že F(hi) = {vi-1,vi}
pro všechna i
![]() <1,n>. Pak posloupnost s=[v0, h1, v1, ... ,
hn, vn] se nazývá orientovaným sledem mezi vrcholy
(uzly) v0 a vn (v tomto pořadí!). Říkáme také,
že v0 a vn jsou orientovaně dostupné, nebo že
vn je orientovaně dostupný
z v0.
Neorientovaný sled, v němž se každá hrana vyskytuje jen jednou, se nazývá cesta.
Cesta, v níž se každý vrchol (uzel) vyskytuje jen jednou, se nazývá prostá cesta.
Platí-li pro prostou cestu s=[v0, h1, v1, ... , hn, vn] rovnost
v0=vn, nazývá se taková prostá cesta kružnice.
Orientovaný sled, v němž se každá hrana vyskytuje jen jednou, se nazývá dráha.
Dráha, v níž se každý vrchol (uzel) vyskytuje jen jednou, se nazývá prostá dráha.
Platí-li pro prostou dráhu s=[v0, h1, v1, ... , hn, vn] rovnost
v0=vn, nazývá se taková prostá dráha cyklus.
<1,n>. Pak posloupnost s=[v0, h1, v1, ... ,
hn, vn] se nazývá orientovaným sledem mezi vrcholy
(uzly) v0 a vn (v tomto pořadí!). Říkáme také,
že v0 a vn jsou orientovaně dostupné, nebo že
vn je orientovaně dostupný
z v0.
Neorientovaný sled, v němž se každá hrana vyskytuje jen jednou, se nazývá cesta.
Cesta, v níž se každý vrchol (uzel) vyskytuje jen jednou, se nazývá prostá cesta.
Platí-li pro prostou cestu s=[v0, h1, v1, ... , hn, vn] rovnost
v0=vn, nazývá se taková prostá cesta kružnice.
Orientovaný sled, v němž se každá hrana vyskytuje jen jednou, se nazývá dráha.
Dráha, v níž se každý vrchol (uzel) vyskytuje jen jednou, se nazývá prostá dráha.
Platí-li pro prostou dráhu s=[v0, h1, v1, ... , hn, vn] rovnost
v0=vn, nazývá se taková prostá dráha cyklus.
Počet hran ve sledu (cestě, dráze, kružnici, cyklu) se nazývá délkou sledu (cesty, dráhy, kružnice, cyklu). Je zřejmé, že existuje-li mezi dvěma uzly sled, může mezi nimi existovat sledů více. Každý z těchto sledů má jistou délku. Mezi těmito délkami (což jsou přirozená čísla) jistě existuje jedna nebo více délek s nejmenší hodnotou. Jsou to délky nejkratších sledů. Nechť G je orientovaný graf. Nechť u a v jsou uzly takové, že existuje sled z uzlu u do uzlu v. Pak délku libovolného nejkratšího sledu z uzlu u do uzlu v nazýváme vzdáleností z uzlu u do uzlu v. Nechť G je neorientovaný graf. Nechť u a v jsou uzly takové, že existuje sled mezi u a v. Pak délku libovolného nejkratšího sledu mezi uzly u a v nazýváme vzdáleností mezi uzly u a v.
Existuje-li pro libovolné dva uzly u a v grafu G sled, pak graf G se nazývá souvislý graf. Graf z příkladu shora není souvislý, protože např. mezi uzly A a E neexistuje sled.
2.5.2 Popis grafu
Popsat (definovat) graf G znamená popsat (definovat) každý element trojice V, E a F. Způsob popisu množin V a E je diskutován v předchozí kapitole, stejně jako definice funkce. Uveďme příklad popisu (definice) grafu G takovým způsobem:
V = { 1, 2, 3, 4, 5 }
E = { a, b, c, d, e, f, g }
F = { [a,{1,2}], [b,[1,2]], [c,{1,3}], [d,{3}], [e,[3,4]], [f,{2,4}], [g,[4,5]] }

Obr. 2.2: Příklad nesouvislého grafu
Grafy však můžeme popsat i pomocí matice sousednosti nebo pomocí incidenční matice.
Matice sousednosti je matice, ve které řádky a sloupce odpovídají uzlům. Platí že, aij=1, je-li mezi Ui a Uj hrana, aij=0, není-li tomu tak. Matice sousednosti odpovídající předchozímu grafu může být taková, jaká je uvedena v tab. 2.3 (pro větší názornost nejsou nulové hodnoty vepsány).
Tab. 2.2: Matice sousednost k obr. 2.2
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 1 | 1 | |||
| 2 | 1 | 1 | |||
| 3 | 1 | 1 | |||
| 4 | 1 | ||||
| 5 |
Zavedení matice sousednosti umožňuje výhodná rozšíření při jejím použití. Plně však odpovídá pouze neorientovaným grafům bez rovnoběžných hran. Matice sousednosti lze však zavést i pro orientované grafy tak, že na uzly umístěné svisle pohlížíme jako na počáteční a na uzly umístěné vodorovně jako na koncové - opět pouze bez rovnoběžných hran. Prvek aij matice je pak roven 1, jestliže existuje hrana mající Ui za počáteční a Uj za koncový vrchol. Taková matice obecně není symetrická. Dále může být maticí sousednosti vyjádřeno ohodnocení (viz dále). Prvek aij pak je roven ohodnocení hrany UiUj. - a to jak pro neorientované (symetrická matice), tak pro orientované grafy.
Incidenční matice je obdélníková matice, ve které sloupce jsou uzly a řádky hrany. Platí, že aij = 1, je-li hrana hi incidentní s Uj, není-li, pak hodnota se rovná 0.
2.5.3 Les, strom
Neorientovaný graf bez kružnic se nazývá les (obr.2.3). Souvislý les se nazývá strom. Orientovaný graf ze nazývá orientovaným lesem, právě když graf vzniklý jeho dezorientací je lesem. Orientovaný graf ze nazývá orientovaným stromem, právě když graf vzniklý jeho dezorientací je stromem.
terminologie (les, strom) vznikla z pohledu na "obrázkové" znázornění grafu. Následující obrázek vpravo ukazuje graf, který je lesem ("má dva stromy"):
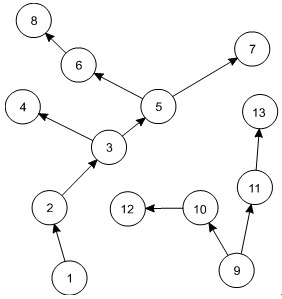
Obr. 2.3: Graf, který je lesem
2.5.4 Ohodnocené grafy
Množství informatických aplikací pracuje s ohodnocenými grafy. Hranově ohodnocený graf je takový, kde každé hraně je přiřazen prvek množiny hodnocení. Uzlově ohodnocený graf je takový, kde každému uzlu je přiřazen prvek množiny hodnocení. V naprosté většině praktických aplikací jsou hrany a vrcholy (uzly) ohodnoceny numericky. Množinou hodnocení je pak množina všech reálných čísel, případně pro konkrétní úlohy množina racionálních, celých nebo i jen přirozených čísel. Pro jeden graf může existovat více než jedno uzlové a (třebas i současně) jedno či více hranových ohodnocení.
Důležitou aplikací v teorii grafů je např. hledání minimální kostry grafu v daném ohodnocení.
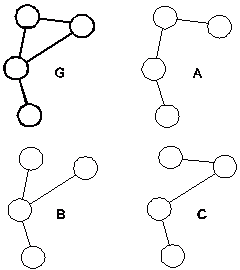
Obr. 2.4: Graf a jeho kostry
Ve vodním hospodářství tomu odpovídá následující – velmi idealizovaná - úloha: Z nově budovaných výrobních míst je zapotřebí odvádět použitou vodu (tj. vybudovat např. kanalizační síť). Technické podmínky i tvar terénu dovolují propojit jednotlivá místa jen podle připojeného plánku; na něm jsou také vyznačeny ceny v [mil.Kč] výstavby jednotlivých úseků (viz obrázek s řešením dole). Je zapotřebí nalézt nejlevnější vedení sítě.Otázku je možno mírně přeformulovat tak, aby se přiblížila teorii grafů: Kolik peněz je minimálně zapotřebí, aby z libovolného místa bylo možno odvést použitou vodu – jinak řečeno, aby každé místo bylo "kanalizačně dostupné" z libovolného jiného místa? Maximální možná síť odpovídá souvislému neorientovanému ohodnocenému grafu. Hledáme jeho podgraf, který jistě nebude obsahovat kružnice (vypuštěním jedné hrany kružnice se dostupnost míst nezmění, ale zlevní se výstavba).
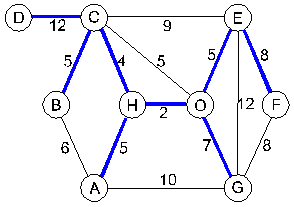
Obr. 2.5: Hledání minimální kostry
Nejprve podle algoritmu zařadíme hranu HO, pak CH. CO však nezařadíme, protože by vznikla kružnice CHOC. Dále zařadíme EO, BC, AH, ale ne AB, protože by vznikla kružnice ABCHA – atd. Nalezená minimální kostra má součet ohodnocení hran (tj. minimální cena výstavby je) 48 [mil.Kč].2.5.5 Kořeny, listy a zdroje
Nechť v
![]() V(G) je vrchol orientovaného grafu G.
Řekneme, že v je kořen grafu G, jestliže každý vrchol grafu
G je orientovaně dostupný z vrcholu
v. Nechť v
V(G) je vrchol orientovaného grafu G.
Řekneme, že v je kořen grafu G, jestliže každý vrchol grafu
G je orientovaně dostupný z vrcholu
v. Nechť v
![]() V(G) je vrchol orientovaného
grafu G. Řekneme, že
v je list grafu G, jestliže vrchol v grafu
G nemá bezprostředního následníka. Nechť v
V(G) je vrchol orientovaného
grafu G. Řekneme, že
v je list grafu G, jestliže vrchol v grafu
G nemá bezprostředního následníka. Nechť v
![]() V(G)
je vrchol orientovaného grafu G. Řekneme, že v je zdroj grafu
G, jestliže vrchol v grafu G nemá bezprostředního předchůdce.
V(G)
je vrchol orientovaného grafu G. Řekneme, že v je zdroj grafu
G, jestliže vrchol v grafu G nemá bezprostředního předchůdce.
Má-li orientovaný graf jediný kořen, je tento kořen zdrojem (a naopak). Má-li orientovaný graf více kořenů, nemá zdroj (a naopak).
- Graf G je kořenovým stromem.
- Graf G má kořen v a do každého vrcholu u různého od v vede právě jediná orientovaná cesta.
- Graf G má kořen a po odstranění libovolné hrany již kořen nemá.
- Graf G má kořen a neobsahuje kružnici.
- Graf G má kořen a má nejvýše n-1 hran.
Důsledek: Kořenový strom má zdroj, a to jediný.
Výrok předchozí věty, že např. "tvrzení 1 je ekvivalentní tvrzení 4" se lépe čte takto: (Graf G je kořenovým stromem) právě tehdy, když (Graf G má kořen a neobsahuje kružnici).
2.5.6 Poznámky ke grafům
Tezaurus si můžeme představit jako strom, jehož vrcholy odpovídají termínům (deskriptorům) a hrany (větve) sémantickým souvislostem mezi termíny. Ve skutečnosti je problém složitější, obvykle nevystačíme jen se vztahy precedence a následnosti, ale využíváme i vztahy průniku
![]() a sjednocení
a sjednocení
![]() .
.
Mezinárodní desetinné třídění představuje stromové klasifikační schéma, např. "vrtný průzkumu" lze vyjádřit stromem s jednoznačným sledem od uzlu 550.822 k uzlu 5: 550.822 vrtný průzkum 550.82 průzkumné metody 550.8 aplikovaná geologie 550. pomocné vědy geologické 55 vědy o Zemi 5 přírodní vědy
2.6 Základy matematické statistiky a geostatistiky
Úvodem je třeba upozornit, že existují určité rozdíly mezi klasickou matematickou statistikou a analýzou geodat pomocí statistických a geostatistických postupů, které vyplývají z vlastností přírodních objektů a z reálných možností jejich zkoumání. Prakticky vždy hodnocení vychází z nehomogenních souborů dat (důsledek různých nositelů - vzorků), které velmi často představují smíšené statistické distribuce. Veličiny, které charakterizují zkoumané objekty, často nejsou statisticky nezávislé. Přírodní objekty se vyznačují zastoupením strukturální i náhodné složky v prostorovém rozmístění hodnot veličin. Lze zkoumat jen v omezeném rozsahu a to vzhledem k dostupnosti a také k nákladnosti geovědních prací. Cíle analýzy a modelování jsou velmi odlišné podle typu objektů a řešeného problému. Uvedené aspekty ovlivňují možnosti a postupy statistické a geostatistické analýzy geodat.
2.6.1 Teorie pravděpodobnosti
Teorie pravděpodobnosti se zabývá studiem hromadných jevů, tj. jevů, které se za určitého komplexu podmínek vyskytují opakovaně ve velkém počtu. Jev představuje přesně vymezenou skutečnost jako výsledek pokusu (experimentu nebo pozorování). Jevy se dělí na jisté (I), nemožné (O) a náhodné (A, B, C, ...). Teprve při hromadném výskytu náhodných jevů se projevují jisté zákonitosti popisované jejich distribucí. To umožňuje odhadovat charakteristické hodnoty (parametry distribucí), předvídat výskyt dalších jevů apod.
Pravděpodobnost P(A) jevu A vyjadřuje kvantitativně možnost jeho uskutečnění. Základní požadavky zobrazení uvádí axiomatická definice pravděpodobnosti:
- Klasická definice pravděpodobnosti:
je-li v jevovém poli n elementárních jevů {E1,E2,...,En}, které jsou za daných podmínek stejně možné, tj. P(E ) = 1/n a rozpadá-li se jev A na m elementárních jevů (počet příznivých případů),
m = n, pak pravděpodobnost jevu A je P(A) = m / nPříklad:
Při průzkumu rudního ložiska bylo odvrtáno 23 vrtů, z nichž 4 zastihly průmyslové zrudnění. Pravděpodobnost výskytu využitelných rud bude P(R) = 4/23 = 0.17 - Geometrická definice pravděpodobnosti: je-li jev
A modelován geometrickou oblastí GA, která je podmnožinou oblasti GI (modelu jistého jevu I),
je pravděpodobnost, že po pokusu nastane jev A P(A)=|GA|/|GI|kde |GA|,|GI| jsou míry oblastí.Příklad:
předpokládáme-li v průzkumné oblasti o ploše 10 km2 výskyt ložiska A modelovaného na povrchu elipsou o rozměrech 500 x 200 m, tj. o ploše cca 78 500 m2, pak pravděpodobnost jeho zastižení bude za předpokladu ploch jako měr oblastíP(A) = 78500 / 107 = 0.008 - Stochastická definice pravděpodobnosti:
nastane-li po n provedených pokusech jev A fn-krát, bude pravděpodobnost jeho výskytuJestliže se náhodný jev A vztahuje jen k určitému systému podmínek, pak se jedná o pravděpodobnost nepodmíněnou.V případě, že závisí ještě na dalším podmiňujícím jevu
 B, jde o pravděpodobnost podmíněnou P(A|B), jejíž hodnota(věta o násobení pravděpodobností). V opačném případě budeJe-li A nezávislý na jevu B, pak platí, že P(AB) = P(A) × P(B)
B, jde o pravděpodobnost podmíněnou P(A|B), jejíž hodnota(věta o násobení pravděpodobností). V opačném případě budeJe-li A nezávislý na jevu B, pak platí, že P(AB) = P(A) × P(B)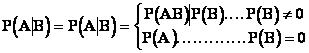 P(AB) = P(A | B) × P(B) = P(B | A) × P(A)V případě sčítání pravděpodobností platí, žeP(A+B) = P(A) + P(B) - P(AB).
P(AB) = P(A | B) × P(B) = P(B | A) × P(A)V případě sčítání pravděpodobností platí, žeP(A+B) = P(A) + P(B) - P(AB).
2.6.2 Náhodná veličina
Lze-li náhodný jev popsat reálným číslem nebo mu číslo přiřadit, pak se toto číslo nazývá hodnotou (realizací) náhodné veličiny (proměnné) U. Množina těchto čísel tvoří obor možných hodnot náhodné veličiny. Náhodné veličiny se obvykle rozdělují na:
- diskrétní, které nabývají konečný počet nebo nejvýše spočetně mnoho hodnot z oboru možných (např. počet známých ložisek v rudním revíru),
- spojité, které mohou nabývat všech možných hodnot z ohraničeného či neohraničeného intervalu (např. obsah užitkové složky v rudě).
Přes nahodilost realizace podléhají náhodné veličiny určitým zákonitostem, které vyjadřuje zákon rozdělení náhodné veličiny U. U diskrétních veličin je plně popsán pravděpodobností jednotlivých hodnot (obr. 2.6 - A), tj. funkcí
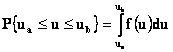
Představu náhodné veličiny lze dále zobecnit na vícerozměrnou náhodnou veličinu, tj. m-rozměrný vektor, jehož prvky jsou náhodné veličiny.
Vedle hustoty pravděpodobnosti (frekvenční funkce) se používá distribuční funkce F(ub), která udává pro každé ub pravděpodobnost nerovnosti u=ub. V případě diskrétních veličin bude
a u spojitých veličin
Body na číselné ose, ve kterých nabývá distribuční funkce jisté zvolené hodnoty, se nazývají kvantily

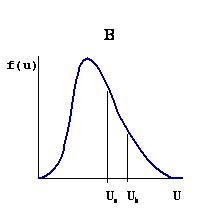
Obr. 2.6: Hustota pravděpodobnosti diskrétní (A) a spojité (B) veličiny
Funkce, které popisují rozdělení pravděpodobnosti náhodné veličiny U, jsou složité a neposkytují jednoduchou koncentrovanou informaci. K tomu slouží parametry rozdělení, které stanovují polohu rozdělení (očekávanou hodnotu, střední hodnotu) E(U) a rozptýlení hodnot kolem ní D2(U). Je třeba mít na paměti, že odhad střední hodnoty a rozptýlení musí vycházet z charakteru statistické distribuce příslušející pozorováním. Střední hodnota diskrétní veličiny je
a spojité veličiny
 ,
,kde a,b jsou meze definičního oboru veličiny U. Další parametry lze odvodit pomocí počátečních Mk a centrálních mk momentů k-tého řádu
a u spojité veličiny
 .
.Odmocnina z rozptylu se nazývá směrodatná odchylka D(U). Dále lze stanovit normované momenty k-tého řádu mk, ze kterých se běžně používá koeficient asymetrie A a koeficient špičatosti (excesu) E
E = m4 - 3 = m4 / m22 - 3 .
je zřejmé, že hustota pravděpodobnosti f(u) je definována jako derivace distribuční funkce F(u) podle proměnné u (pokud derivace existuje).
Dále jsou uvedeny hustoty pravděpodobnosti vybraných typů distribucí náhodných veličin (a je parametr polohy, b2 parametr rozptýlení).
- Hustoty pravděpodobnosti diskrétních veličin.
Rovnoměrné rozdělení R(U;n) p(u) = 1/n ; u = u1, u2, ..., un ; n přirozené
Alternativní rozdělení A(U)Binomické rozdělení Bi(U;n,p) Poissonovo rozdělení Po(U;a)
Poissonovo rozdělení Po(U;a) ; u=0,1,...,n; n přirozené; p
; u=0,1,...,n; n přirozené; p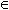 (0,1)
(0,1) ; u=0,1,2,...; a>0
; u=0,1,2,...; a>0
- Hustoty pravděpodobnosti spojitých skalárních veličin
Rovnoměrné rozdělení R(U;a,b)f(u)=1/(b-a);u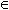 <a,b>;a<b
<a,b>;a<b
Normální rozděleníN(U;a,b2) ;u
;u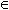 R;b>0
R;b>0
Logaritmicko-normální rozdělení LN(U;a,b2)Exponenciální rozdělení Ex(U;a) ; u>0; b>0f(u) = a×exp(-a×u) ; u≥0; a≥0
; u>0; b>0f(u) = a×exp(-a×u) ; u≥0; a≥0 - Hustoty pravděpodobnosti spojitých vektorových veličin:
Rovnoměrné rozdělení na kružnici R(φ)f(φ) = 1/(2π) ; 0<φ≤2π
Kruhové normální von Misesovo rozdělení M(φ;μ,κ)J0(κ) je modifikovaná Besselova funkce 1. druhu nultého řádu (normalizační faktor) Fisherovo normální rozdělení na kouli F(φ,ψ;κ) ;0<φ≤2π; 0<φ≤2π; κ≥0kde φ je směr a ψ úklon i-tého vektoru, κ parametru koncentrace.
;0<φ≤2π; 0<φ≤2π; κ≥0kde φ je směr a ψ úklon i-tého vektoru, κ parametru koncentrace. ,
,
2.6.3 Náhodná funkce
Náhodnou funkcí se nazývá množina náhodných veličin {ψ(t)}, závislých na reálném parametru t v intervalu T. Je to tedy funkce, která nabývá při i-tém pokusu jistou konkrétní podobu ui(t), která se nazývá realizací náhodné funkce (obr.2.7).
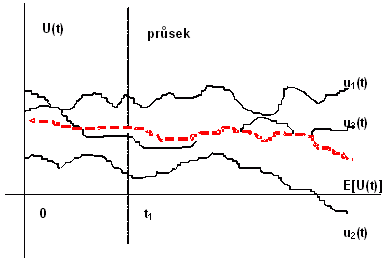
Obr. 2.7: Realizace, střední hodnota a průsek náhodné funkce
Při určité hodnotě parametru (např. t1) získáme průsek náhodné funkce U(t1) a náhodná funkce přejde v náhodnou veličinu. Je-li náhodná funkce invariantní vzhledem k posunu času či polohy, nazývá se stacionární a v opačném případě evoluční. Parametr t se v teorii stochastických procesů označuje jako čas. V geovědách je parametrem nejčastěji poloha na přímce, v ploše či v prostoru. Náhodná funkce, jejímiž parametry jsou prostorové souřadnice X, Y, Z, se nazývá náhodné pole U(X,Y,Z).Na rozdíl od parametrů náhodné veličiny představují parametry náhodné funkce rovněž funkce. Střední hodnota E[U(t)] náhodné funkce U(t) je nenáhodná funkce, která se při každé hodnotě parametru t rovná střední hodnotě odpovídajícího průseku. Je to tedy jistá "střední" funkce, kolem níž kolísají jednotlivé realizace ui(t). Na jejím základě lze zavést centrovanou funkci neboli pulsaci
-
korelační funkce
K(t',t'') = E[U(t') × U(t'')],
- kovariační (autokorelační) funkce K^(t',t'') = E{(U(t')-E[U(t')]) × (U(t'')-E[U(t'')])},
- normovaná autokorelační funkce (korelogram) K^n = K^(t''-t') / K^(0),
-
semivariogram γ(t',t'') = ½ E{[U( t')-U(t'')]2}.
2.6.4 Vybrané pojmy matematické statistiky
Statistický soubor je konečná skupina pozorovaných hodnot jisté náhodné veličiny {u1,u2,...,un}. Hodnoty uspořádané do neklesající posloupnosti
jsou relativní kumulativní četnosti. Pro zjednodušení výpočtů a názornější grafické zobrazení souboru se používá třídní rozdělení četností. Spočívá v rozčlenění variačního rozpětí na zpravidla stejné intervaly - třídy - a nahrazení hodnot souboru náležejících do třídy zastupující hodnotou (zpravidla středem třídy) - třídním znakem. Počet hodnot ve třídě je třídní četnost. Třídní rozdělení četností se graficky zobrazuje histogramem nebo polygonem absolutních nebo relativních četností. Histogram a polygon četností představují empirickou frekvenční funkci, histogram a polygon kumulativních četností empirickou distribuční funkci. Vypovídací schopnost histogramu silně závisí na správné volbě počtu tříd, který by měl ležet v rozmezí 7 až 20. Stanovení počtu tříd vychází z variačního rozpětí, z počtu pozorování apod. Cílem statistického zpracování souboru je stanovení ukazatelů polohy (aritmetického průměru, mediánu apod.) a ukazatelů rozptýlení (rozpětí, rozptylu, směrodatné odchylky), které jsou definovány analogicky jako výběrové charakteristiky. U statistického souboru se dvěma a více argumenty se dále stanovují ukazatelé statistické závislosti (kovariance, koeficient korelace).
Množina všech možných hodnot náhodné veličiny, která může být konečná či nekonečná, se nazývá základní soubor (populace) s rozdělením pravděpodobnosti R(U;μ,σ2). Konstanty vyjadřující charakteristické vlastnosti základního souboru, se nazývají parametry nebo teoretické charakteristiky (střední hodnota μ, rozptyl σ2 atd.). Náhodný výběr je n nezávislých hodnot náhodné veličiny, vybraných ze základního souboru tak, aby výběr nebyl závislý na vlastnostech hodnoceného objektu a na subjektivní úvaze řešitele. Náhodné výběry se konvenčně dělí na výběry malé (n<30) a velké (n≥30). Náhodný výběr popisují výběrové charakteristiky polohy, rozptýlení apod., které jsou samy náhodnými veličinami, neboť závisejí na konkrétním výběru.
Úkolem statistické indukce je usuzovat z vlastností výběru na vlastnosti základního souboru. Přitom se kladou na bodové odhady parametrů, které jsou ve skutečnosti pouze a jenom jejich aproximací a jsou tedy zatíženy jistou chybou, určité požadavky. Za „dobrý” odhad považujeme takový, který vyhovuje požadavkům nestrannosti (tzn. střední hodnota diference odhadu a její chyby má být nulová), konzistence (s růstem rozsahu výběru roste pravděpodobnost, že se odhad blíží parametru), vydatnosti (jde o nejlepší nevychýlený odhad parametru) a robustnosti (odhad je stabilní i při ne zcela splněných požadavcích na pravděpodobnostní vlastnosti veličiny, je odolný proti vlivům odlehlých pozorování a proti chybám měření). Z uvedených důvodů se často používá intervalový odhad parametrů základního souboru - tzv. konfidenční interval, o kterém předpokládáme, že s předem zvolenou vysokou pravděpodobností (označovanou jako konfidenční koeficient) obsahuje odhadovaný parametr. Ve sféře geověd jsou intervalové odhady velmi užitečné vzhledem ke značnému stupni neurčitosti poznání přírodních jevů a rekonstrukce procesů jejich formování. Mají velký význam např. při hodnocení spolehlivosti výpočtů zásob nerostných surovin, technicko-ekonomických hodnoceních nebo při projektování průzkumných a těžebních prací.
Významnou součástí zpracování dat je testování statistických hypotéz. Pod statistickou hypotézou se rozumí jakýkoliv předpoklad o typu rozdělení pravděpodobnosti, o parametrech základního souboru, o charakteru závislostí náhodných veličin apod. Test statistické hypotézy je pravidlo, které na základě poznatků zjištěných z náhodného výběru umožňuje rozhodnout, zda má být ověřovaná hypotéza přijata (považována za možnou) nebo zamítnuta (považována za nepravděpodobnou). Nejde o důkaz platnosti či neplatnosti hypotézy! Při testu se rozlišuje hypotéza nulová H0 (testovaná) a hypotéza alternativní H1. Postup testování sestává z těchto kroků:
- formulace nulové H0 a alternativní H1 hypotézy,
- volba hladiny významnosti α (udává výši rizika zamítnutí správné testové hypotézy),
- volba testové charakteristiky a její výpočet,
- porovnání hodnoty testové charakteristiky s kritickou hodnotou,
- přijetí nebo zamítnutí nulové hypotézy.
Při testování může podle obr. 2.8 vzniknout chyba I. druhu (zamítnutí správné nulové hypotézy) nebo chyba II. druhu (přijetí nesprávné nulové hypotézy).

Obr. 2.8: Druhy chyb při testování hypotéz
Vedle testování hypotéz na základě pevného rozsahu statistického výběru existuje odlišně přístup k testování hypotéz, který přináší sekvenční analýza. Základní myšlenkou sekvenčních metod je uskutečnit právě tolik pozorování, aby byl splněn požadavek určité předem zadané přesnosti odhadu nebo aby byla maximalizována přesnost při zadaných nákladech na pozorování. Takový přístup odpovídá realitě, neboť všechny průzkumy se provádějí sekvenčním postupem: v průzkumu se pokračuje, dokud se nenahromadí dostatek poznatků nutných pro rozhodnutí nebo dokud jsou finanční prostředky.
2.6.5 Geostatistická analýza dat
Termínem geostatistika označil Matheron (1963) aplikaci teorie náhodných funkcí na popis a oceňování přírodních objektů, které lze charakterizovat distribucí hodnot tzv. regionalizovaných - prostorových veličin (např. fyzikálních charakteristik, obsahu užitkových a škodlivých složek v ložiskovém tělese)
kde ui,ui+h jsou hodnoty veličiny U ve vzdálenosti h. Experimentální semivariogram je empirická realizace určovaná z množiny pozorování u1,u2,...,un
kde m je počet dvojic pozorování v určitém směru objektem.
Experimentální semivariogram je pro návazné úvahy aproximován teoretickým modelem γ*(h). Modely semivariogramů se dělí do několika skupin a to na:
- modely přechodového typu, tj. s prahem (sférický, kvadratický, gaussovský, exponenciální),
- modely bez přechodu (lineární, logaritmický),
- modely s oscilujícím prahem (sinový, cosinový),
- čistě náhodný model.
Jako příklad je dále uveden často se vyskytující sférický model s vysvětlením používané terminologie (obr.2.9).
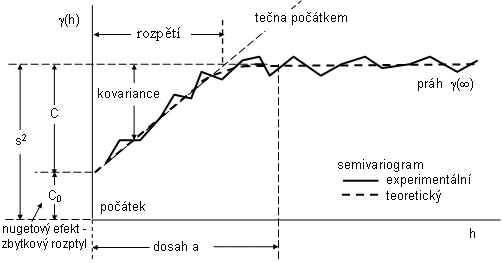
Obr. 2.9: Terminologie popisu semivariogramu
Pomocí studia semivariogramů lze ocenit kontinuitu pole (dosahem u přechodových semivariogramů a koeficientem absolutního rozptylu u semivariogramů bez přechodu), nehomogenitu pole (podle oscilace prahu), nestacionaritu pole (podle parabolické deformace v oblasti prahu) a izotropii či anizotropii pole (vyhodnocením směrových semivariogramů).
Rovnice hlavních typů semivariogramů (použité označení odpovídá obr.2.10):Sférický semivariogram (Matheronův)
 , a
= 1.5 d
, a
= 1.5 dExponenciální semivariogram (Formeryho)
Logaritmický semivariogram (de Wijsův)
 , g=π/ω
, g=π/ωkde ω je polovina periody, Cosinový semivariogram
V případě závislosti veličin Uk, Ul lze zobecnit představu strukturální funkce na koregionalizaci, tj. definování vzájemného semivariogramu
Základním úkolem geostatistiky je poskytnout odhady hodnoty veličiny v jistém bodě v0, elementární ploše δS či bloku δV studovaného náhodného pole V. Nejlepší odhad průměrné hodnoty u* veličiny U, který splňuje obecně požadované podmínky nestrannosti E(u*-u) = 0 a minimálního rozptylu D2(u*-u) = min, je určován z hodnot ui, (i=1,2,3,...,m) v okolí odhadu podle vzorce
za podmínky
V případě kvazistacionarity pole v okolí odhadu se váhy λi určí minimalizací rozptylu odhadu
kde A je odhadovaný element (bod, plocha, blok) a γ průměrná hodnota semivariogramu. Průměrné hodnoty semivariogramu se vypočtou podle vztahu
kde jeden konec vektoru (b-b´) popisuje nositel vb a druhý nositel vb' (obr. 2.10). Numerická aproximace je
b,b' jsou středy jistých úseků nositelů v a v'.
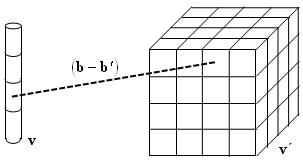
Obr. 2.10: Princip výpočtu průměrné hodnoty semivariogramu
Pomocí metody Lagrangeových multiplikátorů μ dostaneme po úpravách soustavu rovnic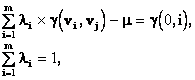
Indikátorové krigování vychází ze skutečnosti, že každou funkci f[Uk(X,Y,Z)] lze vyjádřit pomocí indikátorů. Je-li náhodnou funkcí proměnná, která nabývá konečný počet hodnot

Spojitou proměnnou lze převést na indikátorovou pomocí indikátorové funkce
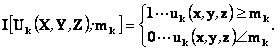
Indikátorová proměnná je pak základem pro výpočet semivariogramu γI(h) a návazných odhadů krigováním
se soustavou
Disjunktivní krigování, které bylo vyvinuto pro řešení problému ocenění vytěžitelných zásob, je podle Davida (1988) teoreticky lepší metoda odhadu. Vyžaduje ale striktní stacionaritu náhodného pole. Cílem je získat podmíněnou distribuci dílčích jednotek pole reprezentovaných fyzickými body, kterou lze vyjádřit jako
kde Hi(U) jsou Hermitovy polynomy i-tého řádu a n+1 potřebný počet členů rozvoje,
h=n/2 pro n sudé a h=(n-1)/2 pro n liché. Každý koeficient Ci je odhadován nezávisle (proto název disjunktivní) řešením jednoduchého krigovacího systému
ve kterém váhy
![]() se určí řešením soustavy
se určí řešením soustavy
kde
![]() je i-tá mocnina korelace mezi normalizovanými hodnotami vzorků a
je i-tá mocnina korelace mezi normalizovanými hodnotami vzorků a
![]() bloku a vzorků.
bloku a vzorků.

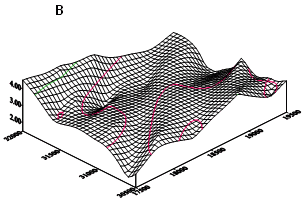
Obr. 2.11: Příklady využití krigování: A – výsledky blokového krigování; B - plocha modelovaná bodovým krigováním (Staněk, 1999)
Zásadní předností krigovacích postupů je skutečnost, že:- vycházejí ze strukturálních charakteristik náhodného pole,
- respektují prostorové rozmístění míst pozorování,
- uvažují velikost odhadovaných elementů pole a vzorků,
- vedle odhadu u* určují i jeho rozptyl σk2.
2.6.6 Prostředky pro statistickou a geostatistickou analýzu dat
Softwarový trh nabízí velké množství programových prostředků, určených pro statistickou a geostatistickou analýzu geodat. Vedle toho existuje řada volně dostupných softwarových produktů tohoto typu. Při výběru produktů je nutno jednak prostudovat jejich možnosti (tj. aplikované metody průzkumové, statistické a geostatistické analýzy a způsoby grafické prezentace), jednak uvážit vlastní požadavky a pochopitelně i finanční možnosti. Řada postupů je zabudována do jiných programových prostředků, jako jenapř. Surfer, produkty firmy Rockware apod.
2.7 Průzkumová analýza geodat
Je skutečností, že neexistuje jednotně a univerzálně použitelný návod pro analýzu dat. Jsou pouze známa pravidla a omezení, která je při zpracování nutno respektovat. Z tohoto důvodu se v posledních desetiletích začaly rozvíjet jednoduché popisné techniky (často empirické povahy), mezi které Tukey (1977) zahrnuje techniky pro ulehčení popisu dat a pro pochopení statistických souvislostí. Jde o průzkumovou analýzu dat, která vychází z velmi volných předpokladů (např. spojitost, existence momentů, derivovatelnost). Tato analýza využívá hlavně metody grafické analýzy a robustní metody založené na pořadových statistikách (kvantilové míry), které jsou definovány pomocí variační řady
Průzkumová analýza dat je tedy jistý filozofický přístup, který naznačuje, jak analyzovat data, co v nich hledat a jak interpretovat zjištěné poznatky. Tyto myšlenky a postupy rozvíjela řada dalších autorů, např. Hoaglin et al. (1983), Velleman a Hoaglin (1981) atd.
2.7.1 Vizualizace dat
Základem postupů průzkumové analýzy je grafické zobrazení dat formou grafů rozptýlení, kvantilových grafů, krabicových grafů, grafů pro vyjádření stupně symetrie, grafů typu ”stromu s listy”, histogramů a polygonů četností, resp. i pravděpodobnostních grafů. Podle Hoaglina et al. (1983) jde v zásadě o zjištění:
- do jaké míry je rozdělení dat symetrické,
- v jakém rozmezí se data pohybují,
- zda se v datech vyskytují vybočující pozorování,
- v jakých úsecích dochází ke kumulaci dat - zda se v datech vyskytují ”prázdné” úseky.
2.7.1.1 Grafy rozptýlení
Nejjednodušším způsobem vizualizace dat je jejich vynesení na číselnou osu. Klasický graf rozptýlení, označovaný také jako bodový diagram, je v principu projekcí kvantilového grafu. Základní výhodou grafu je jednoduchost a kompaktnost, nevýhodou překrývání dat stejné hodnoty. Proto se body odpovídající stejným hodnotám vynášejí nad sebe (vznikají tak sloupečkové grafy) nebo se vynášejí náhodně v určitém zvoleném intervalu. Z grafů rozptýlení lze určit rozmezí a přibližně střed dat, lokální změny koncentrace dat, přibližně symetrii empirické distribuce a odlehlá pozorování.
2.7.1.2 Kvantilové grafy
Kvantilový graf znázorňuje průběh výběrové kvantilové funkce Qi(Pi), jejímž odhadem jsou pořadové statistiky ű(i) pro pravděpodobnost Pi= i/(n+1), resp. při malém výběru (n<30) Pi= (i-0.5)/n, kde i je pořadí hodnot u(i) ve variační řadě. Kvantilový graf se doplňuje obdélníky, které charakterizují oblasti vybraných kvantilů - kvartilů, oktilů a sedecilů (obr. 2.12). K jejich sestavení je třeba vypočítat potřebné kvantilové hodnoty podle vztahu
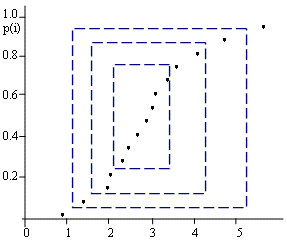
Obr. 2.12: Kvantilový graf s kvantilovými obdélníky
Podle rozmístění kvantilových obdélníků a vývoje výše uvedených statistik lze odhalit základní statistické rysy hodnoceného výběru dat:- symetrické jednovrcholové rozdělení:
- kvantilové obdélníky jsou rozmístěny v sobě symetricky,
- polosumy jsou přibližně konstantní,
- šikmost je přibližně nulová;
- nesymetrické jednovrcholové rozdělení
- kvantilové obdélníky jsou nesymetrické (u kladně asymetrického rozdělení jsou vzdálenosti mezi levými stranami výrazně menší),
- polosumy se mění (u kladně asymetrického rozdělení rostou s poklesem p),
- relativní šikmost není nulová,
- vícevrcholové rozdělení
- se projevuje úseky s téměř horizontálním průběhem v kvartilovém obdélníku;
- rozdělení diskrétní veličiny
- graf se skládá pouze z vertikálních úseků;
- odlehlé hodnoty
- se projeví subhorizontálním průběhem grafu vně sedecilového obdélníku (pozor u silně asymetrických rozdělení!).
2.7.1.3 Krabicové grafy
Krabicové grafy (box plot) patří mezi základní techniky průzkumové analýzy. Jsou běžně používaným způsobem sumarizace dat a vizualizace základních charakteristik hodnoceného výběru, tj. polohy, rozptýlení, šikmosti a odlehlých pozorování. Při konstrukci krabicového grafu se nejprve určí medián ű0.5 a oba kvartily ű0.25 = QL a ű0.75 = QU. Dále se vypočítávají hranice vnitřních HL, HU a vnějších VL, VU hradeb
HU = QU + 1.5 (QU - QL)
VL = QL - 3.0 (QU - QL)
VU = QU + 3.0 (QU - QL)
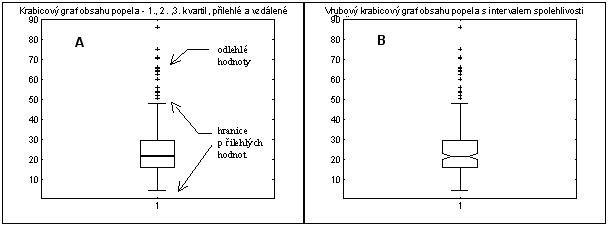
Obr. 2.13: Krabicový graf a vrubový krabicový graf (Honěk, Staněk, 1998)
2.7.1.4 Grafy pro vyjádření stupně symetrie
Symetrie rozdělení dat je důležitou charakteristikou výběrů. Pokud je rozdělení přibližně symetrické, lze snadno použít robustní metody odhadu parametrů rozdělení a provádět další statistické výpočty. Jednoduchý způsob posouzení symetrie je založen na transformovaných veličinách
2.7.1.5 Histogram četností
Běžně používaným postupem vizualizace empirických distribucí na základě třídního rozdělení četností je histogram (obr. 2.14). Vypovídací schopnost histogramu silně závisí na volbě počtu tříd, který by měl ležet v rozmezí 7 až 20. Vyhovující počet lze stanovit podle variačního rozpětí
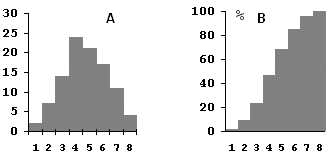
Obr. 2.14: A - histogram absolutních četností; B - histogram kumulativních relativních četností
2.7.1.6 Pravděpodobnostní graf
poskytuje jednoduchou možnost vizualizace empirické distribuční funkce a její porovnání s některou teoretickou distribucí. Jde v podstatě o kvantil-kvantilový graf, který využívá souřadného systému (u,up) v případě normální nebo (log u,up) v případě lognormální distribuce, kde up jsou probity, tj. upravené kvantily teoretické distribuce. Testovaná empirická distribuce se v případě shody s teoretickou zobrazí v grafu jako přímka (obr.2.15).
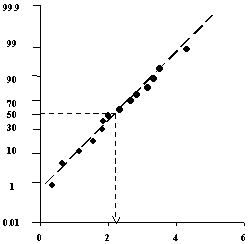
Obr. 2.15: Pravděpodobnostní graf
2.7.2 Robustní odhady statistických charakteristik
Robustní odhady statistických charakteristik jsou založeny na lineárních kombinacích kvantilů empirických distribucí. Pro ocenění charakteristiky polohy se vedle obecně známého mediánu Me, pro který platí, že P(ui = ű0.5 ) = 0.5, se používají další kvantilové odhady střední hodnoty. Velmi stabilní odhady poskytuje trimean
 ,
,kde g=int(n.α)+1, p=g-n.α, α se obvykle volí 0.1 (jde vlastně o aritmetický průměr). Podobně se určuje winzorizovaný průměr
 ,
,kde
2.7.3 Ocenění závislosti veličin
Předběžnou informaci o typu a charakteru závislosti veličin U a O, která je potřebná pro volbu postupu statistického zpracování, získáme z korelační tabulky a korelačního diagramu, ve kterém se může projevit i homogenita či heterogenita výběru pozorování. Těsnost vztahu lze jednoduše ocenit pomocí neparametrického Blomqvistova kritéria. (obr. 2.16). Rozdělíme-li korelační diagram rovnoběžkami s osami v mediánech obou veličin a označíme-li podle obr. 4.6 počet bodů v I. a III. kvadrantu n1 a počet bodů ve II. a IV. kvadrantu n2, pak mírou závislosti je veličina
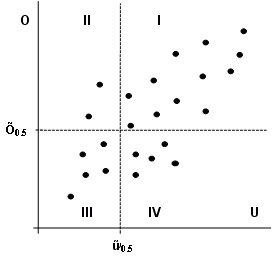
Obr. 2.16: Orientační ocenění těsnosti vztahu pomocí Blomqvistova kritéria
Na závěr je nutno uvést, že existuje řada dalších metod vizualizace dat a velké množství robustních statistik, založených na kvantilech empirických distribucí, které lze nalézt ve speciální literatuře. Poněvadž průzkumová analýza stále ještě není běžně využívána, bylo cílem této kapitoly ukázat, jak můžeme jednoduchými postupy získat první představu o zpracovávaných datech, na jejímž základě lze provést seriozní statistickou a geostatistickou analýzu dat. Proto také byly uvedeny alespoň některé vztahy pro určení robustních statistik.
2.8 Postupy statistické a geostatistické analýzy geodat
Ukazuje se, že z hlediska analýzy geodat je možno vyčlenit určité úlohy, které jsou společné různým typům geovědních problémů. Rodionov et al.(1973) je nazvali typové úlohy. Za hlavní můžeme považovat: popis typu statistické distribuce veličin, odhad středních hodnot a variability veličin včetně ocenění spolehlivosti odhadů, řešení problému odlehlých pozorování, ocenění a popis vzájemných vztahů veličin, analýzu struktury a popis průměrných charakteristik polí veličin a ocenění shody či rozdílů geologických objektů. Řešení těchto úloh je komplikováno jednak nestardandním charakterem geodat, jednak způsoby jejich sběru, tj. systémem pozorování (průzkumným systémem). Dále je věnována pozornost problémům, se kterými se v praxi setkáváme.
2.8.1 Statistická analýza
Jednou ze základních otázek statistického rozboru je studium charakteru statistické distribuce. Jen na základě správného popisu distribuce, který musíme prověřit pomocí testů shody, lze odhadnout statistické charakteristiky a realizovat statistické soudy. Při zpracování výsledků pozorování nejrůznějších veličin popisujících geologická tělesa se zjistilo, že značný počet jejich empirických distribucí nevyhovuje běžně uvažovanému normálnímu rozdělení N(U;μ,σ2), ze kterého také vychází většina statistických postupů, ale že vykazují více či méně asymetrickou distribuci (a to převážně kladně asymetrickou). Proto se pro popis využívají různé transformace veličin, např. obecná logaritmická v = ln(a+bu), která vede k velmi často používanému obecnému lognormálnímu rozdělení LN(U;μ,σ2,a,b), nebo obecná mocninná transformace
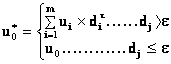
(Optimální hodnoty konstant použité transformace lze určit pomocí účelové funkce symetrizační nebo normalizační (obr. 2.17),
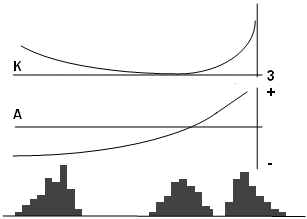
Obr. 2.17: Optimální transformace podle Box-Coxova principu
Při řešení praktických úloh se poměrně často setkáváme s případem cenzorování statistické distribuce, tj. podmíněného rozdělení veličiny U nabývající hodnot možných, jehož popis uvádí např. Hald (1949). To znamená, že určitý počet n0 pozorování ui z celkového počtu n hodnot leží pod mezí ma nebo nad mezí mb. Např. v chemických analýzách vzorků se vyskytují hodnoty označené symboly "0", "stopy", "<ma", ">mb" (ma je mez citlivosti a mb mez rozlišitelnosti analytické metody). Postup odhadu statistických charakteristik musí tuto skutečnost respektovat a to zejména v případech významnějšího zastoupení takovýchto hodnot.
Empirické distribuce mají často polymodální charakter, vyvolaný smíšením hodnot dvou nebo více základních souborů (např. hodnot normálního a anomálního chemického či fyzikálního pole, tj. hodnot horninového pozadí a lokální anomálie). Statisticky jde o smíšené rozdělení
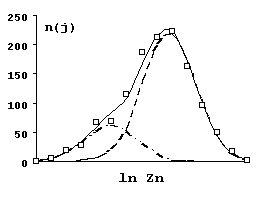
Obr. 2.18: Separace bimodální distribuce Zn v bilančních úsecích 6.-9. patra ložiska Horní Benešov (Schejbal et al.,1977)
Při posuzování výsledků pozorování se často setkáváme s výskytem hodnot, které se nápadně odlišují od ostatních. Tyto hodnoty jsou v geovědách známy pod označením extrémní (uraganní) hodnoty, ve statistice jako odlehlá pozorování. Vyloučíme-li případy hrubých chyb, pak před námi stojí problém posuzování reálných velmi nízkých nebo velmi vysokých hodnot, které přinášejí značné obtíže při odhadu statistických charakteristik (např. při výpočtu zásob značně variabilních rudních ložisek barevných a drahých kovů). Způsoby zpracování extrémních hodnot lze rozlišit na empirické (hodnoty jsou považovány za objektu vlastní nebo jsou jistým způsobem nahrazovány např. střední hodnotou, průměrem sousedních hodnot, nejvyšší ”normální” hodnotou apod.) a na matematicko-statistické, kdy jsou extrémní hodnoty vyčleňovány buď na základě kritérií odlehlých pozorování (např. Grubbsova testu či Dixonova kritéria) nebo pomocí separace smíšených distribucí. Problém reálných extrémních hodnot korektně a úplně řeší geostatistika v rámci variografie (efekt zbytkového rozptylu) a krigování (váha pozorování na odhad), jak je uvedeno v kapitole 2.4.
Reálné geologické objekty a procesy jsou popisovány řadou veličin U1, U2, ..., Um . Z teoretického i praktického hlediska nás zajímá, existuje-li mezi nimi určitý vztah, jaká je těsnost a forma vztahu. Tyto vztahy mají v převažující většině případů charakter statistické závislosti, kdy se se změnou hodnoty jedné veličiny mění podmíněná střední hodnota veličiny druhé nebo její rozptyl (skedastická závislost). Posouzení míry a formy závislosti veličin je náplní korelační a regresní analýzy, v případě studia veličin kvalitativní povahy asociační analýzy.
Běžně se studuje dvourozměrný statistický soubor N(U,V; μu, μv, σu, σv, σu,v), kde μu, μv jsou střední hodnoty, σu, σv směrodatné odchylky a σu,v je kovariance. Pro posouzení se nejčastěji používají parametrické míry závislosti, např. Pearsonův koeficient korelace, jehož použití vyžaduje splnění podmínek binormalitu rozdělení a existenci přímkové závislosti veličin. V případě odlišného typu distribuce je nutno provést vhodnou transformaci dat, aby byly splněny uvedené podmínky. Před věcnou interpretací výsledků je třeba vždy prošetřit statistickou významnost vypočtené hodnoty korelačního koeficientu. Obvyklou mírou těsnosti vztahu veličiny V na řadě jiných veličin U1, U2, ... ,Um je koeficient mnohonásobné korelace, který má podobné vlastnosti a podmínky použití, jako koeficient párové korelace.
Obecně lze doporučit využití metod pořadové korelace, které nejsou závislé na typu rozdělení a které umožnují analýzovat i semikvantitativní data a data s možným výskytem extrémních hodnot. Obvykle používanou mírou Spearmanův koeficient pořadové korelace Tyto míry mají jen velmi volné předpoklady použití a proto se při řešení geologických problémů dobře uplatňují.
Vedle těsnosti vztahu je pro řešení řady otázek nutno popsat i formu vztahu veličin. To umožňuje regresní analýza. Jejím cílem je popsat vztah mezi závisle proměnnou veličinou V a nezávisle proměnnými veličinami {U1, U2, ... }. Obecně používaný postup vychází z využití metody nejmenších čtverců. Při studiu statistické závislosti dvou veličin se často doporučuje stanovit obě možné regresní funkce V = f(U) a U = f(V), které v případě přímkové závislosti tvoří tzv. regresní nůžky, které při vysoké těsnosti vztahu se k sobě blíží. Dále je výhodné stanovit tzv. redukovanou hlavní osu regrese . Princip stanovení uvedených závislostí je zřejmý z obr.2.19.
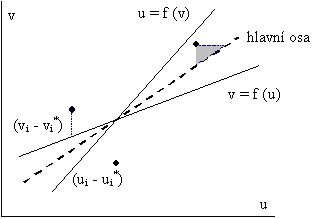
Obr. 2.19: Princip odhadu regresních závislostí
V praxi často pracujeme s celou řadou veličin kvalitativní povahy, které lze členit do dvou či více kategorií. Často je užitečné posoudit a kvantifikovat jejich vztahy, resp. vztahy s veličinami kvantitativními, které je ale nutno pro tuto analýzu také přetransformovat na veličiny kvalitativní. To je náplní asociační analýzy.
Korelační a regresní analýza poskytuje při uvážlivém použití velmi efektivní nástroje studia struktury složitých přírodních objektů a procesů. Uvedené postupy totiž zkoumají a popisují pouze vnější formální vztahy, pod kterými se ale nemusejí skrývat reálné příčinné souvislosti. Formální vztah může být vyvolán definicí veličin, heterogenitou souboru dat, společnou závislostí na další veličině apod. Tedy sebesilnější statistické závislosti nemohou určit a objasnit příčinný vztah veličin. Idea příčiny musí vycházet z vlastní analýzy problému a z pečlivého posouzení výsledků (obr. 2.20). Při hodnocení statistických vztahů se totiž neustále pohybujeme mezi nebezpečím jejich přecenění nebo nedocenění, kdy je především nutno vyloučit možné zdánlivé vztahy, výstižně nazývané ”nonsense correlations”.
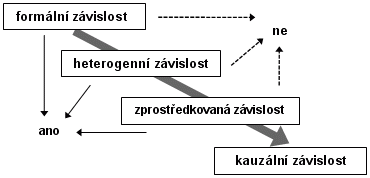
Obr. 2.20: Schéma logického rozboru výsledků analýzy závislostí
2.8.2 Popis polí geovědních veličin
Jednou ze základních úloh analýzy dat je popis struktury a modelování polí geologických veličin. Úkoly analýzy struktury pole pro potřeby modelování zahrnují popis kontinuity, homogenity či nehomogenity, stacionarity či nestacionarity a izotropie či anizotropie pole. Některé z těchto úkolů lze řešit pomocí statistických postupů (např. vymezení statisticky homogenních oblastí pole, studium anizotropie pole pomocí směrové analýzy variability apod.), komplexní řešení je založeno na geostatistické strukturální analýze, tj. na analýze semivariogramů, které v sobě obsahují všechny potřebné strukturální informace. Způsoby modelování geologických polí, které tvoří běžnou součást analýzy dat, lze podle použitého principu rozdělit do třech skupin.
2.8.2.1 Popis pole po kvazihomogenních úsecích
vychází z tradičního způsobu popisu zkoumaných geoobjektů v geologii. Studované pole se popisuje po úsecích, jejichž hranice lze určit podle věcných hledisek (např. hranic horninových komplexů, strukturně-tektonických jednotek, zón výrazných změn hodnot pole apod.). Po vymezení kvazihomogenních bloků je nutno prověřit statistickou homogenitu odpovídajících výběrů pomocí statistických kritérií a poté každý blok charakterizovat obvyklým statistickým způsobem, tj. odhadem středních hodnot Ej(Ui), rozptylů Dj2(Ui) a vzájemných vztahů veličin Ui, (i = 1,2,...,m) v každé j-té části pole.
2.8.2.2 Popis pole globálními funkcemi
Při popisu pole globálními funkcemi se považuje plošné nebo prostorové rozložení hodnot proměnné veličiny U za funkci polohy, tj. za regresní funkci plošných nebo prostorových souřadnic. Nejpoužívanější typ tzv. trendové analýzy je zpravidla založen na polynomickém mnohonásobném regresním modelu

kde φj jsou polynomické funkce souřadnic. Volba vhodného typu regresní rovnice představuje značný problém a řešení má dosti subjektivní ráz. Teoreticky by měla odrážet faktory, které kontrolují prostorovou distribuci hodnot studované veličiny (Whitten - Koelling, 1973). Prakticky se vychází z vizuálního porovnání výsledných trendových map se vstupními daty a s mapami reziduí a dále z vyhodnocení vhodných statistických ukazatelů přiléhavosti trendové plochy k experimentálním údajům (např. indexu mnohonásobné korelace a determinace, testu statistické významnosti členů regresního modelu, minimálního součtu kvadrátů odchylek apod.). Porovnávají se řešení při postupně zvyšovaném stupni polynomu podle uvedených kritérií, někdy pomocí tzv. mozaikového trendu (rozčlenění plochy na dílčí). Pro volbu „nejlepšího” tvaru regresní rovnice je nejvhodnější procedura kombinované krokové regrese. S rozvojem metod trendové analýzy se dospělo k poznatku, že při studiu jevů s oscilující povahou (např. zvrásněné plochy) je vhodnější použit trendový model typu harmonické, resp. polyharmonické funkce, která vedle základního trendu (střední hodnoty) umožňuje popsat i lokální periodické složky a charakter korelovatelnosti hodnot
2.8.2.3 Popis pole lokálními funkcemi
Lokální modely vytvářejí morfologii empirické křivky či plochy postupnou interpolací nebo aproximací pomocí funkcí, jejichž koeficienty jsou odvozeny z pozorování v dílčích úsecích pole. Často používané jsou procedury klouzavých průměrů a příbuzných aproximačních vzorců (např. Shepparových), které v podstatě náleží k metodám filtrace polí. Velmi rozšíženým postupem jsou metody inversních vzdáleností. Jde o vážené průměry, ve kterých vystupuje jako váha pozorování jistá mocnina τ převrácené hodnoty vzdálenosti di pozorování ui
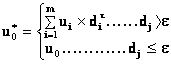
kde ε→0 v závislosti na měřítku. použití uvedených postupů vznikají problémy vyvolané jednak anizotropií pole, jednak nerovnoměrným rozložením průzkumných bodů. Pro zabránění vlivu „shluků” pozorování se zavádějí různé omezující testy, zpravidla založené na výběru zvoleného počtu nejbližších pozorování a kvadrantových či oktantových výběrech. Vliv anizotropie pole lze eliminovat pomocí anizotropní oblasti výběru pozorování pro odhad.
Podobně se využívají splinové funkce, které se vyznačují hladkostí a minimální křivostí a které jsou schopny postihnout i velmi variabilní rozložení hodnot veličiny. Obvykle je využívána kubická funkce, kdy v každém úseku <xi, yj, xi+1, yj+1> je morfologie plochy dána funkcí
přičemž spojitost a hladkost se zajišťuje pomocí prvých a druhých derivací. Funkce musí splňovat podmínku
 ,
,kde δu je chyba stanovení modelované veličiny a K minimalizační konstanta (při K=0 jde o interpolaci, při K>0 o aproximaci). Problém představuje stejně jako v případě krigování možná existence diskontinuit v ploše. Velmi úspěšné jsou krigovací metody, založené na teorii náhodných funkcí. Pro modelování ploch se aplikuje bodové krigování, jehož formulace je analogická jako v případě blokového krigování popsaného v kapitole 2.6. Zásadní předností tohoto postupu je skutečnost, že vychází ze strukturálních charakteristik pole (homogenity, anizotropie, stacionarity) a respektuje prostorové rozmístění míst pozorování.
2.8.3 Analýza příbuznosti geoobjektů
Velmi významnou součást analýzy geodat je hodnocení příbuznosti přírodních objektů. Obecně se jedná o klasifikační úlohu, kdy prověřujeme hypotézu o vzájemné shodě či rozdílu hodnocených objektů, hodnotíme shodu objektu s určitým typovým objektem či hledáme objekty sobě nejbližší. Nejjednodušším typem takovéto úlohy je klasifikace do dvou tříd. Úlohu můžeme samozřejmě rozšířit na případy porovnávání a klasifikace většího počtu objektů.
2.8.3.1 Základní statistické klasifikační postupy
se opírají o statistické testy různého typu, prověřující hypotézy o shodě rozptylů, středních hodnot, typu rozdělení apod. Při jejich používání je nezbytné respektovat podmínky aplikace, které jsou uváděny v každé učebnici matematické statistiky.
2.8.3.2 Multivariační klasifikační postupy
mohou při respektování podmínek použitelnosti mnohem úplněji popsat studované objekty s rozdíly mezi nimi. Např. studium petrochemické příbuznosti vyvřelých komplexů bude úspěšnější, bude-li využívat všech složek sledovaných při silikátové analýze, než studium založené pouze na jedné složce. Podobně vymezení komplexní geochemické anomálie je z hlediska lokalizace možného ložiska nadějnější, než posuzování anomálií jednotlivých prvků. Vícerozměrná náhodná veličina (náhodný vektor) U = {U1, U2, ..., Um} je charakterizována střední hodnotou (vektorem středních hodnot)

jejíž diagonální prvku jsou rozptyly veličin U1, U2, ... , Um. Prošetření shodu nebo rozdílu výběrů popsaných vícerozměrnou veličinou může být založeno na ověření nulové hypotézy o shodě vektorů středních hodnot, o shodě kovariačních matic a konečně o shodě vektorů středních hodnot i kovariačních matic současně. Tyto hypotézy se ověřují pomocí různých kritérií, jako je např. Hottelingovo kritérium T2 o shodě průměrů, Mahalanobisova všeobecná vzdálenost D2 vážených průměrů či Kullbakovo kritérium pro ověření shody kovariačních matic.
Obecná analýza rozptylu
se používá k ověření hypotézy a shodě průměrů Ek(U) vícerozměrných veličin v k skupinách. Obdobně jako v případě jednofaktorové analýzy rozptylu se snaží popsat celkový rozptyl jako sumu rozptylu uvnitř skupin a mezi skupinami a ocenit jejich významnost.
Diskriminační analýza
je jednou z řady multivariačních klasifikačních technik, která umožňuje: zjistit rozdíly mezi hodnocenými objekty, které vytvářejí v m-rozměrném prostoru shluky , jejichž poloha je charakterizována multivariačním průměrem; stanovit hranice mezi skupinami objektů pomocí diskriminační funkce (nadplochy), která odděluje shluky; třídit další objekty pomocí stanovených hranic. To znamená, že pomocí diskriminační analýzy se řeší jednak problém existence a oprávněnosti odlišování tříd objektů, jednak klasifikace nových objektů do jedné z vymezených tříd (obr.2.10). Pro řešení konkrétního problému jsou při diskriminační analýze
Sdružovací (shluková, clusterová) analýza
zahrnuje velkou řadu procedur, které bez apriorního definování klasifikačních tříd podle určitého pravidla postupně sdružují objekty na základě jejich vzájemné podobnosti. Cílem je vytvoření struktury studovaného souboru objektů a klasifikace dalších. Sdružovací procedury mohou třídit objekty popsané jak kvantitativními, tak kvalitativními veličinami a vytvářet hierarchické či nehierarchické struktury objektů.
Hierarchické metody se dělí na metody sdružovací a metody nehierarchické. Sdružovací metody jsou rozšířenější, neboť výsledné grafické znázornění příbuznosti objektů dendrogramem (znázorňuje vztahy mezi skupinami) nebo dendrografem (postihuje i vztahy uvnitř skupin) je velmi názorné a snadno pochopitelné i pro toho, kdo není seznámen s matematickou podstatou metody (obr. 2.21). Nehierarchické metody vycházejí z počátečního rozkladu množiny objektů do k shluků a definovaných zárodků, tj. pro ně typických objektů nebo bodů ( např. těžišť). Počáteční rozklad je pak v iteračním procesu zlepšován pokud je to možno.
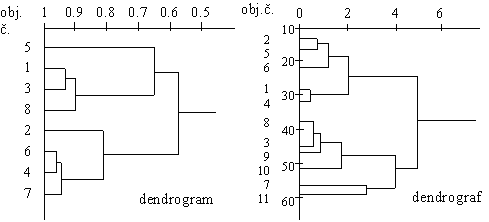
Obr. 2.21: Grafické znázornění hierarchického sdružování
Dosud uvedené metody sdružovací analýzy přiřazují objekty ke shlukům jednoznačně, což je často v rozporu s přirozenou povahou objektů, vyznačující se nejednoznačností. Proto se využívají metody fuzzy shlukování (Zadeh, 1965), ve kterých je příbuznost mezi objektem a shlukem vyjadřována pomocí funkce příslušnosti.
Je důležité zdůraznit, že sdružovací analýza je obdobně jako další klasifikační metody v podstatě empirická technika bez jednotného matematického základu. Zejména nejsou stanovena kritéria pro výběr vhodného algoritmu sdružování a pro prověření reálnosti vyčleněných skupin. Metody sdružovací analýzy jsou citlivé na odchylky od normality rozdělení a výskyt odlehlých pozorování (důsledek nutnosti počítat aritmetické průměry z hodnot proměnných, ze vzdálenosti objektů apod.). Proto se zavádějí postupy shlukování založené na odhadu středních hodnot pořadovými statistikami (nejčastěji mediánem).
Faktorová analýza
se používá pro řešení různých klasifikačních problémů a pro vytváření hypotéz o studovaném problému, objektu či jevu. Pojem „faktorová analýza” zahrnuje řadu variant, z nich jsou nejvíce používány metoda hlavních os - hlavních komponent. Cílem faktorové analýzy je zpracovat a redukovat matici dat U = {ui,j} s n pozorováními a m veličinami tak, aby vznikla co nejjednodušší struktura tzv. faktorů (obr. 2.22). V případě analýzy typu R, kdy n pozorování tvoří shluk v m-rozměrném prostoru proměnných, to jsou nové „hypotetické proměnné stojící v pozadí”, při analýze typu Q, kdy pozorování vytvářejí shluk m proměnných v n-rozměrném prostoru pozorování, jsou to „typy objektů”. Utvořená struktura musí obsahovat co největší množství informace obsažené v původních datech. Výsledkem faktorové analýzy je tedy buď vyseparování hypotetických faktorů nebo faktorových skóre.
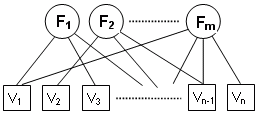
Obr. 2.22: Princip odvozování hypotetických faktorů
2.9 Matematická statistika v dokumentografii
Značná část problémů, spojených se zpracováním průzkumných a vědeckých informací, se dá charakterizovat jako řešení problému zobrazit výsledky celého průzkumného programu, výzkumného úkolu, dokumentu apod. pomocí co nejmenšího počtu slov a jiných znaků (symbolů, čísel) a utvoření souhrnných závěrů. V oblasti zpracování výsledků pozorování a měření je situace zřejmá. Metody matematické statistiky jsou dnes široce využívány v průzkumné a ložiskové geologii, inženýrské geologii, hydrogeologii atd.
Matematicko-statistické metody se používají i v dokumentografii a bibliografii, zejména při automatickém indexování, metodě citačních vazeb, permutovaných rejstříků, tvorbě a aktualizaci tezauru apod. Při tom je přípravnou operací sestavení tabulky frekvence a pořadí slov v textu. Frekvenci slov a jejich pořadí vyjadřuje Zipfův zákon, podle kterého je frekvence a pořadí slova přibližně konstantní
Základní postupy knihovnické a informatické statistiky patří mezi techniky průzkumové analýzy a základní statistické analýzy dat. Typické úlohu jsou:
- zpracování dat do tabulek absolutních a relativních četností;
- grafická prezentace dat (sloupkové grafy, řádkové grafy, kruhové grafy apod.);
- pořádkové charakteristiky průzkumové analýzy (vybrané kvantily jako základ pro ukazatele polohy, rozptýlení a šikmosti);
- výběrové statistické charakteristiky polohy, rozptýlení a šikmosti;
- metody statistické indukce (bodové a intervalové odhady parametrů základního souboru, studium závislostí, testování hypotéz).

Obr. 2.23: Příklad grafické prezentace bibliografických údajů. Počet abstraktů z referátového časopisu INDEX 1986 (upraveno dle Königové et al., 1988)
Použití metod průzkumové a matematické statistiky vede ke snížení redundance (nadbytečnosti, obecnosti) informací ze zpracovávaného dokumentu a ke zvýšení relevance uživatelem požadované informace.
2.10 Principy studia, popisu a modelování geoobjektů
Geoobjekty představují z hlediska metodologie studia, popisu a modelování složitý špatně organizovaný systém, sestávající z relativně samostatných dílčích elementů, které jsou organizovány souhrnem vzájemných vazeb do určité, hierarchicky uspořádané prostorové struktury. Tato struktura je odrazem zpravidla velmi komplikovaných interakcí fyzikálních, chemických a biologických pochodů v průběhu procesů, které probíhaly v určité fázi vývoje jisté oblasti, např. geotektonické jednotky. To znamená, že v každém objektu, např. v horninovém tělese, musí existovat určitá zákonitost v prostorovém rozmístění hodnot veličin jej charakterizujících, která je ale komplikována řadou rušivých vlivů a elementů. Ty se projevují částečně jako nehomogenity na dané úrovni pozorování - tj. v určité průzkumné etapě - zjistitelné, částečně jako náhodné fluktuace. Nejobecnějšími vlastnostmi geoobjektů tedy budou:
- smíšený charakter prostorové distribuce hodnot veličin popisujících objekt, který zahrnuje nenáhodnou složku podléhající geologickým zákonitostem a složku náhodnou,
- nehomogenní rozmístění hodnot příslušných veličin v objektu, přičemž posouzení homogenity - přesněji řešeno kvazihomogenity - či nehomogenity je v proporcionálním vztahu k měřitku pozorování,
- anizotropie prostorové distribuce hodnot veličin, neboť prostorová struktura objektů vznikala pod vlivem usměrněných energetických procesů spojených s transportem hmoty.
2.10.1 Geoobjekty jako náhodné pole
Kterýkoliv geoobjekt si můžeme představit jako kvazihomogenní náhodné pole V, t.j. část geologického časoprostoru
Často se pro účely stanovení hranic objektu definuje geometrická funkce příslušnosti bodu v k tělesu V
Je-li potřebné popsat časové změny charakteristik objektů (např. při těžbě ložiska. při studiu hydrogeologických objektů či geodynamických jevů), použijeme vyjádření pomocí funkce prostorových souřadnic a času
2.10.2 Modely geoobjektů
Sestavování modelů geologických objektů (těles, procesů či jevů) je běžnou součástí práce po dlouhá desetiletí, neboť geologické modely ”jsou klíčem k jakémukoliv průzkumnému programu” (Babcock, 1984), tedy základem veškeré aplikované geologie. Jejich konstrukce byla založena především na mentální analýze. Byla tak silně závislá na odborné erudici a zkušenostech autora, jehož induktivně-deduktivní postupy byly a jsou často obtížně popsatelné a algoritmizovatelné. Široce se využíval princip analogie, který je jedním z hlavních metodologických principů dodnes. S rozvojem základních přírodních věd a nezbytných technik a hardwaru se modelování, založené na využití matematických metod a počítačových technologií, velmi rozvinulo a rozšířilo.
Základem použití matematických postupů při řešení geovědních problémů je převedení reálných objektů do formy abstraktních matematických modelů. Je nezbytné zdůraznit, že modelování je v prvé řadě určováno vlastnostmi geoobjektů. V podstatné míře je ale ovlivňování přijatým geometrickým modelem objektu. Ten je závislý na systému pozorování a představách řešitele a v řadě případů je modifikován oborově jinými faktory (např. v případě ložisek nerostných surovin naturálními a hodnotovými ukazateli využitelnosti nerostné suroviny). Posledně uvedené vlivy mohou v některých případech nabývat podstatný, resp. určující rozměr. Právě reálnost a hodnověrnost geometrického modelu geoobjektu představuje jeden ze základních problémů matematicko-geologického modelování. Jestliže je přijatý geometrický model založený na chybné koncepci geologické stavby objektu, pak seberafinovanější matematický model nemůže tuto chybu eliminovat.
V zásadě můžeme rozlišit prostorové modelování morfologie geoobjektů a modelování jejich ”vnitřních” atributů. Modelování morfologie může být vedle tradičních metod geometrie ložisek (aplikace deskriptivní geometrie) založeno na metodách dvou a trojrozměrné počítačové grafiky (vrstevnicové, drátové a objemové modely). Modelování vnitřních atributů geoobjektů vychází vedle empirických pravidel z využití matematicko-fyzikálních teorií polí a teorie náhodných veličin a náhodných funkcí. Vede tedy k modelům deterministickým, statistickým, geostatistickým a empirickým. Deterministické modely jsou využívány např. v geofyzice, hydrogeologii, geomechanice a v některých případech i v ložiskové geologii a aplikované geochemii. Jsou založeny na přesně popsatelných vztazích mezi nezávislými a závislými proměnnými, ze kterých lze odvodit jednoznačné důsledky za známých podmínek, takže chování daného systému je možno plně predikovat v čase i v prostoru. Z předchozího textu je ale zřejmé, že tento přístup představuje značné zjednodušení a že je použitelný jen za jistých podmínek. Velmi rozšířené jsou statistické modely, neboť funkční vyjádření polí sledovaných veličin a jejich vzájemných vztahů je obtížné a často prakticky nerealizovatelné. Za reálnější se považují geostatistické modely, založené na náhodných funkcích (polích), které mají schopnost postihnout jak prostorovou strukturu objektů, tak jejich náhodnou složku. Velmi časté jsou také empirické modely, které určitým matematickým aparátem popisují objekt na základě jisté apriorní představy autora bez teoretického zdůvodnění.
Pro efektivnost matematicko-geologického modelování mají velký význam datové modely. Modelování musí být založena na věcně opodstatněných koncepčních modelech, které vycházejí jednak z předem formulovaných cílů prací, jednak z obecných zákonitostí formování a vývoje geoobjektů. Jejich praktickou aplikací jsou modely sběru dat – průzkumné modely. Vztahy mezi uvedenými modely a etapami analýzy dat jsou znázorněny schématem na obr. 2.24.
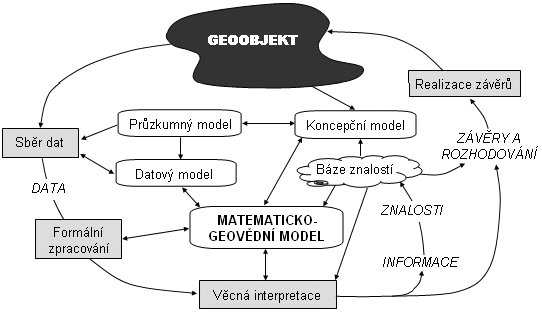
Obr. 2.24: Vztahy mezi tvorbou modelů a etapami zpracování dat
Významnou složkou celého procesu modelování je báze znalostí. I když tento termín je vlastní sféře znalostního inženýrství, resp. konkrétně expertním systémům, má své obecné opodstatnění. Je důležitou složkou procesu modelování, neboť je základem tvorby koncepčních modelů a na nich budovaných matematicko-geovědních modelů.
Složitost přírodních objektů vyžaduje rozumné zjednodušení modelů, neboť jinak by řešení bylo příliš komplikované nebo dokonce nemožné. Tento fakt dobře vyjadřuje princip inkompatibility, zformulovaný Zadehem (1973): ”Roste-li složitost systému, klesá naše schopnost formulovat přesné a významné soudy o jeho chování, až je dosaženo hranice, za níž jsou přesnost a relevantnost prakticky vzájemně se vylučující charakteristiky.” Obecným problémem je skutečnost, že v každém objektu existuje určitá ”bariéra náhodnosti”, která nedovoluje ani při sebedokonalejším systému pozorování jít za hranice jeho poznatelnosti (Schejbal, 1982a). Bylo už konstatováno, že naše soudy o zkoumaných přírodních objektech jsou zatíženy větší či menší neurčitostí. Ta nevadí v koncepčních modelech vytvářených v přirozeném jazyce, který se vyznačuje vágností sémantiky a schopností s vágními pojmy pracovat. Při tvorbě matematicko-geologických modelů a procedur analýzy dat představuje neurčitost značný problém. Právě proto se začaly používat statistické a geostatistické postupy a v posledních letech i další přístupy, jako je teorie fuzzy množin a lingvistických proměnných.
Všechny přírodní systémy jsou ve své podstatě dynamické, vyvíjejí se v prostoru a v čase. Dynamika procesů, resp. jim odpovídajících geoobjektů, kolísá ve velice širokých mezích, od velmi vysoké (hydrologie, vulkanologie, seismologie), přes dynamiku pozorovatelnou v „lidském měřítku” (hydrogeologie, vlivy poddolování, sesuvy) až po velmi malé (např. pohyb litosférických desek, vrásnění).
Dynamické systémy se vyznačují prouděním a transportem. V geologických systémech je transport hmoty podstatným aspektem všech dynamických složek systému (např. difúze iontů v krystalové mřížce minerálů, šíření polutantů v podzemních vodách, transport klastických částic říčním tokem, přínos sloučenin kovů hydrotermálními roztoky do vhodných struktur horninového prostředí, pohyb magmatu, konvekční proudy v astenosféře atd.). V rámci dynamických systémů jsou tedy transportovány různé materiály v rozdílném prostředí (homogenním či nehomogenním, porézním či kompaktním (tab. 2.4).
Tab. 2.4: Příklady dynamických systémů v geologických vědách
| kategorie | typ materiálu | proudění a transport | |
| v nepórézním prostředí | v pórézním prostředí | ||
| I | voda | vodní toky, mořské proudy | proudění podzemních vod |
| ropa a plyn | pohyb v ložiskových strukturách | ||
| led | pohyb ledovců | ||
| II | horniny | plastické deformace hornin, deformace solných dómů | |
| III | horninové částice | sesuvy, turbiditní proudy, bahnotoky, přenos | |
| IV | horninové taveniny | efuzivní horniny | intruzivní horniny |
| V | vodní roztoky za vysokých pt-podmínek | hydrotermální a metamorfní roztoky | |
| vodní roztoky za nízkých pt-podmínek | proudění mořské vody v pánvích vzniku evaporitů | vznik akumulací U, V, Sr atd. z podzemních vod | |
Při studiu a popisu dynamických systémů se používají různé teoretické principy často v kombinaci s heuristickými postupy, neboť řada procesů není stále ještě dostatečně poznána. Lze však říci, že bez ohledu na tuto skutečnost existují možnosti matematického modelování procesů proudění a difuze.
Dynamické systémy mohou být lineární či nelineární, časově závislé nebo nezávislé. U reálných systémů je většina dějů popsána nelineárními závislostmi, ale pro praktické použití se nahrazují lineárními. Jejich konkrétné vyjádření vychází v principu ze základní diferenciální rovnice kde
Φ je přenosová funkce. Případ využití je uveden na obr. 2.25.
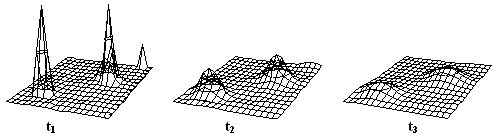
Obr. 2.25: Simulace vývoje geochemických sekundárních aureol
Uvedená rovnice je pro konkrétní problémy vhodně upravována. Např. Hobbs (1997) použil pro vyjádření poměru mineralizace Qm výraz