12. Stabilitní poměry a výpočty
12.1 Použité metody MKP- modelový program Plaxis
Pro výpočty bylo využito programového systému PLAXIS 2D. Tento programový systém byl speciálně vyvinut pro deformační a stabilitní analýzu geotechnických úloh a je založen na numerické metodě konečných prvků. Jedná se o komplexní výpočetní systém, který umožňuje simulaci nelineárního chování zemin. Dává možnost modelovat jak hydrostatické, tak i hydrodynamické účinky vody v zeminách a také vzájemnou interakci mezi konstrukcí (výztuží, kotvou, geotextílií, stěnou apod.) a zeminou.
12.1.1 Základní charakteristika a možnosti
programového systému
Součástí programu je automatický generátor sítě konečných prvků s možností globálního či lokálního zjemnění sítě. Kromě trojúhelníkových prvků s 6-ti uzly (s polynomem 2. stupně pro trojúhelníky) jsou k dispozici rovněž 15-ti uzlové trojúhelníkové prvky s kubickým polynomem (Brinkgueve, 1998).
K řešení úloh je možné použít jak základní Mohr-Coulombův konstitutivní model, tak i model pro konsolidované zeminy s měkkou konzistencí typu Cam-Clay.
Stupeň bezpečnosti (Safety factor) je v tomto systému definován jako poměr mezi dosažitelnou (vrcholovou) smykovou pevností a minimální smykovou pevností nutnou pro udržení rovnováhy. Ze zavedené standardní Coulombovy podmínky obdržíme stupeň bezpečnosti ve tvaru (Brinkgueve, 1998):
Safety factor = 
,
kde: c, j - jsou vstupní
pevnostní parametry,
cr, jr - jsou snížené pevnostní parametry,
sn - je skutečné normálové napětí.
12.1.2
Hlavní
modelové prvky programového systému PLAXIS 2D
Při zahájení práce na novém projektu je nutné nejprve zadat geometrii modelu. Je nutné docílit toho, aby byl model dostatečně velký a reprezentativně postihoval modelovanou oblast. Tento model pak sestává z bodů (points), linií (lines) a shluků (clusters). Body ohraničují linie na jejich začátcích a koncích a mohou být také využity k definování polohy kotev, bodů napětí a k lokálnímu zjemnění sítě. Linie jsou využívány ke stanovení hranic modelu a mimo jiné i k definování diskontinuit vrstevnatého prostředí. Shluky jsou oblasti úplně ohraničené liniemi. Program Plaxis automaticky rozpoznává základní shluky ve vstupní geometrii. V oblasti tohoto základního shluku by pak měly být vlastnosti zeminy homogenní. Shluk je pak možno považovat za část vrstvy zeminy a vlastnosti tohoto základního elementu je možné aplikovat na shluky prvků s obdobnými parametry (Brinkgueve, 1998).
Po zadání geometrie modelu program automaticky generuje síť konečných prvků jež obsahuje tři typy komponentů:
- Prvky (elements) – během generování sítě jsou shluky (clusters) rozděleny do trojúhelníků. Tyto trojúhelníky pak podle požadované přesnosti obsahují 6, nebo 15 prvků.
- Uzly (nodes) – 6-ti uzlový trojúhelník se skládá ze 6 uzlů (a), 15-ti uzlový pak z 15 uzlů (b)
a)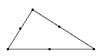 
b) 
·
B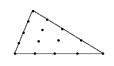ody napětí (stress points) –
6-ti uzlový trojúhelník obsahuje 3 napěťové body (a), 15-ti uzlový pak 12
napěťových bodů (b)
a)
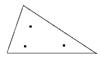b)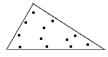 
12.1.3 Výpočetní metodika programového systému
PLAXIS 2D
Výpočetní
metodika programového systému PLAXIS vychází z metody konečných prvků.
Tato metoda je variační metodou, která předpokládá nahrazení kontinuálního
pevného tělesa konečným počtem diskrétních elementů (obvykle trojúhelníků). Ty
jsou pak mezi sebou spojeny konečným počtem uzlových bodů. Na každém z těchto
konečných prvků aproximujeme přesné řešení posunutí, jemuž odpovídající napětí
splňuje diferenciální rovnici rovnováhy, vhodnou aproximační funkcí. Konkrétní
tvar aproximační funkce (aproximačního polynomu) závisí na typu konečného prvku
a počtu uzlových bodů jež danému prvku přísluší. Náhradní aproximační funkce
definuje jednoznačně stav posunutí uvnitř každého konečného prvku pomocí
posunutí uzlů tohoto prvku. Posunutí uzlů jsou pak základními neznámými
parametry úlohy a spolu s původními deformacemi a vlastnostmi materiálu na
základě zvoleného konstitutivního stavu charakterizují napěťový stav jak uvnitř
prvku, tak i na jeho hranách.Výsledkem vztahu mezi složkami posunutí uzlů a
mezi silami jimi vyvolanými ve všech uzlech prvku (síly nahrazují napětí
působící na hranách elementu) je pak tzv. matice tuhosti, jejíž každý řádek je
tvořen koeficienty rovnic, které vyjadřují rovnováhu sil od napětí
v prvku, a to v jednotlivých uzlech ve směru souřadných os. Celý
problém je tak redukován na řešení soustav lineárních algebraických rovnic,
přičemž tato soustava se stává regulérním zadáním příslušných okrajových
podmínek (geometrických, resp. silových).
Výchozí
vztahy deformační teorie:
Základní rovnicí je rovnice rovnováhy:
, 
…vektor složek
napětí, 
…vektor sil
.
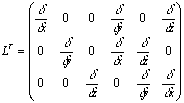Dále
platí kinematický vztah : 
.
Na základě Galerkinova variačního principu
s využitím předchozích základních vztahů lze formulovat stav rovnováhy
následovně : 
je tu variace posunů.
Po
aplikaci Greenovy věty na předchozí rovnici dostáváme následující vztah,
vyjadřující princip virtuální práce: 
,
kde vektor
hraničních sil 
je zohledněn
v hraničním integrálu.
Rozvoj napěťového stavu lze vyjádřit přírůstkovým
integračním předpisem: 
, kde 
je přírůstek napětí odpovídající krátkému časovému úseku,
vektor 
představuje neznámý
aktuální napěťový vztah, 
pak známý
vektor napětí v předchozím kroku.
Aktuální napěťový stav je tedy určen následující rovnicí:
.
Posuny na daném elementu jsou
vyjádřeny pomocí aproximačního polynomu s využitím diskrétních uzlových
hodnot (vektor
) následovně: 
Po dosazení do kinematického vztahu
dostáváme: 
Určující
rovnici pro stanovení neznámého vektoru 
lze pak vyjádřit ve tvaru:
Úpravou
získáme: 
Po dosazení vztahu mezi přírůstkem
vektoru posunutí a přetvoření dle zvoleného konstitutivního modelu 
do předchozí rovnice a
po úpravě platí:
,
kde
K je matice tuhosti, 
přírůstek vektoru
posunutí, 
vektor vnějších sil, 
vektor vnitřních sil
příslušející kroku i.
Dynamický model
Jedním
z přídavných modelů zmíněného programového systému je dynamický výpočetní
modul, umožňující modelovat vliv dynamického zatížení v geotechnice a
podzemním stavitelství. Příčiny uvažovaného dynamického zatížení mohou být jak
přirozené (zemětřesení), tak antropogenní - spojeny s lidskou činností
(vliv těžkých mechanismů, dopravy, technologie výstavby pilot, trhací a
destrukční práce jak v podzemí, tak i na povrchu).
Základní výchozí vztah pro modelování dynamického
chování je následující:
Mu´´ + Cu´ + Ku = F
M… hmotnostní matice
C… útlumová matice
K… matice tuhosti
F… silový vektor
Hmotnostní
matice M zahrnuje vliv hmotnosti jak
samotné zeminy, tak i vody a případné geotechnické konsolidace a vychází
z Newtonova zákona F=m.a. Útlumová matice C je definována pomocí Rayleighovy rovnice materiálového tlumení:
C = akM + bkK
Kromě
standardně požadovaných vstupních dat pro statický výpočet je nutno
v případě dynamických výpočtů dále zadat hranice absorbce, umožňující
modelovat útlum vln, procházejících horninovým prostředím. V opačném případě
by totiž, v kontrastu se skutečností, došlo k reálnému zpětnému
odrazu vln od hranic modelu a ke zkreslení výsledků výpočtů. Dále je třeba
charakterizovat samotné dynamické zatížení. U jednozdrojových typů vibrací je
nutno zadat amplitudu a frekvenci vlnění, v případě modelování vlivu
zemětřesných jevů programový systém umožňuje využít tzv. SMC (Strong Monitor
CR-ROM) souborů. Tento typ souborů je využíván v U.S.Geological Survey
National Strong-monitor Program k záznamu zemětřesných dat a obsahuje hodnoty
zrychlení popř. rychlosti nebo časové řady deformací.
Uvedený
dynamický programový modul tedy umožňuje modelovat šíření dynamického zatížení
horninovým prostředím, vyhodnotit účinky dynamického zatížení na geotechnické
konstrukce, stanovit dosah vlivu dynamického zatížení. Výsledky modelování pak
mohou rovněž přispět k optimálnímu rozmístění monitorovacích zařízení,
umožňujících objektivnější posouzení dynamických vlivů a včasné vyhodnocení
varovných stavů.
12.2 Použité metody mezní
rovnováhy
V této kapitole
jsou popsány metody mezní rovnováhy, které byly použity pro stabilitní analýzu
svahových modelů.
V programu
GeoStar, kterým byly výpočty
prováděny, je zařazena řada výpočetních metod pro výpočty metodami mezní
rovnováhy. Mimo standardní a známé metody jsou zde obsaženy i modifikované
metody. Mají proti metodám, ze kterých jsou odvozeny, některé výhody a zároveň
mají i robustnější výpočetní algoritmy. Metody mají za sebou v době
uvedení programu GeoStar 3.3 (resp. 3.4) na trh téměř 15 let vývoje a nasazení
při výpočtech na extrémně rozsáhlých a rizikových lokalitách. Tato
kapitola obsahuje základní informace o definici jednotlivých metod (Bartůněk,
2001).
Názvy
jednotlivých metod jsou v programu použity v podobě, pod kterou byly
publikovány (tab. 12.2.1).
Tab 12.2.1 Význam značek a symbolů v názvech metod (Bartůněk,
2001)
|
E-Efektivní napjatost |
K – Kruhová smyková plocha |
J – Jednoduchá metoda |
N – Nerozlišené smykové par. |
|
nebo |
nebo |
nebo |
nebo |
|
T – Totální napjatost |
O – Obecná smyková plocha |
P – Přesná metoda |
R – Rozlišené smykové par. |
Ve
vzorcích popisujících jednotlivé metody jsou použity symboly z Tab. 12.2.2
s jednotným významem pro kruhové i obecné plochy.
Tab 12.2.2 Význam symbolů použitých ve vzorcích (Bartůněk,
2001)
|
g |
objemová tíha |
bi , li |
šířka proužku, délka smykové plochy v i-tém proužku |
|
j‘i , j‘i,r |
efektivní úhel vnitřního tření, vrcholová a reziduální hodnota |
hi |
výška proužku ve střednici |
|
c‘i , c‘i,r |
efektivní soudržnost, vrcholová a reziduální,totální soudržnost |
ti,R , ti,L |
svislá vzdálenost působiště vnitř. sil od středu báze proužku zleva a zprava |
|
ksx , ksy , kw |
seismické součinitele ve směru x a y, součinitel vnějších horizontálních sil |
Wi |
tíha proužku |
|
Q |
základní úhel vnitřních sil |
Hi |
horizontální síla (z externích hor. sil) |
|
fi,R , fi,L |
distribuční funkce zprava a zleva |
Ni |
normálová síla |
|
Tol |
nastavení tolerance výpočtu |
Ti, Ti,r |
tangenciální síla – smykový odpor, neporušený, porušený proužek |
|
Fm, Ff , F |
stupeň bezpečnosti z momentové a silové výminky, celkový stupeň bezpečnosti |
Zi,R,x ,Zi,L,x |
meziproužkové síly zprava a zleva |
|
R |
poloměr smykové kružnice |
u , U |
pórový tlak, vztlaková síla |
|
xs , ys , xi,
yi |
souřadnice středu sm. kružnice, respektive momentového bodu, i-tého proužku |
ru |
součinitel pórového tlaku |
|
ai |
sklon smykové plochy v i-tém proužku od vodorovné |
i |
index proužku |
Obr 12.2.1 Schéma výpočtu
stability (Bartůněk, 2001)
Pettersonova
metoda
Klasická jednoduchá proužková metoda pro výpočty
mezní rovnováhy je v programu zavedena ve standardní podobě, kdy výsledný
stupeň stability je počítán ze vzorce
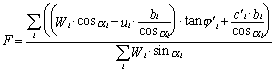
Tato metoda neuvažuje vliv jednotlivých proužků
navzájem.
Bishopova metoda
V GeoStaru
je zabudována tzv. redukovaná Bishopova metoda, kde výpočet stupně
stability pro kruhové smykové plochy vychází ze vzorce
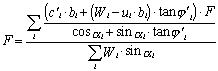
a stupeň stability se počítá pomocí Banachovy věty
o pevném bodu. Předchozí vzorec lze formálně upravit na tvar
a následně je konstruována posloupnost
Jestliže je splněna podmínka 
, kde Tol je hodnota nastavená uživatelem programu, pak
prohlásíme poslední vypočtenou hodnotu Fi za hledaný stupeň stability F = Fi. Tato metoda oproti Pettersonově
metodě uvažuje vliv jednotlivých proužků navzájem (Bartůněk, 2001).
Metoda
EKP
Obr 12.2.2 Schéma výpočtu
stability metodou EKP (Bartůněk, 2001)
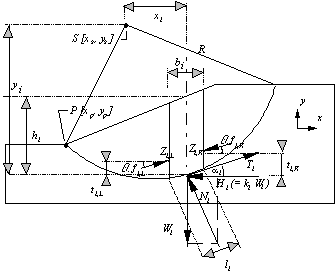
Pro kruhovou
smykovou plochu zavádí do výpočtu meziproužkové síly a splňuje všechny výminky
rovnováhy.
Ze silových podmínek rovnováhy plyne:
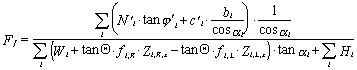
Z momentové výminky pak:
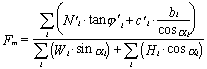
Pro výpočet meziproužkových sil je v programu použit rekurzivní
vztah:
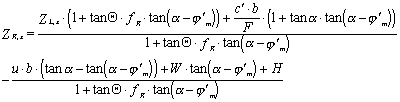
v němž pro: 
normálová síla je počítána ze vztahu:
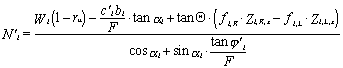
Vlastní postup výpočtu je následující:
· podle věty o pevném bodu nalezneme pro dané Q hodnoty Fm a Ff z výminek pro rovnováhy,
· z podmínky Fm=Ff získáme kritérium pro výpočet Q metodou sečen (Bartůněk, 2001).
Poloha působišť meziproužkových sil je určena vzorcem:
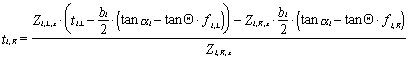
12.3 Stabilitní výpočty
12.3.1
Zadání modelu
Modelování na
této lokalitě mělo za cíl stanovit smykovou plochu, stupeň stability, body
plasticity, horizontální posuny, vertikální posuny, totální posuny,
horizontální posuny na námi zvolených místech (řezech) a deformaci svahu.
Samotné modelování probíhalo v místě, na kterém bylo provedeno geofyzikální měření, extenzometrické měření a taktéž zde byl proveden geologický řez svahu (příloha č. 5.1 a 5.2). Takto může dojít ke konfrontaci metod provedených na tomto úseku.
V matematických modelech na dané lokalitě byly simulovány dvě různé úrovně hladiny podzemní vody. Jako první byla modelována varianta, která simulovala prostředí před započetím sanačních prací. Zde byly využity výsledky z vrtných a laboratorních prací zpracovaných ve zprávách firmy GEOtest Brno, a.s. Protože provedené laboratorní zkoušky na odebraných vzorcích zeminy nezastihly celý geologický profil, muselo se také využít tabulkových hodnot pro zeminy a horniny z normy ČSN 731001. Odebrání vzorku zemin bylo provedeno na smykové ploše a v jejím blízkém okolí. V době vrtných a laboratorních prací nebylo počítáno s možností využití tohoto modelového programu. Mechanické vlastnosti zemin a hornin použité k těmto modelům jsou uvedeny v následující tabulce (Tab. 12.3.3.1). Hladina podzemní vody v této první variantě je odečtená z vrtných sond J2, J3 a J4. Jedná se zde o napjatou hladinu, která po odvrtání těchto vrtů vystoupala od 1,9 m (vrt J2 ) do 0,55 m pod povrchem (vrt J3).
Jako druhá varianta
modelování byla provedena simulace po dokončení sanačních prací. Použité
hodnoty vzorků zemin jsou uvedeny v tabulce (Tab.12.3.3.2). Výška hladiny
podzemní vody je volena jako střední hodnota z posledních měření
v hydrogeologických vrtech HV-1, HV-2 a HV-3.
Tyto dvě uvedené varianty byly ještě rozvedeny do dvou různých modelových situací. První z nich zachycovala již zmíněné varianty bez jakéhokoliv vnějšího (okolního) přitížení. Druhá modelová situace byla provedena i s přitížením na samotném těle sesuvu. Jednalo se o silnici třetí třídy (ulice Hlubočická), na které se před sanačními pracemi projevily prvotní příznaky svahové deformace. Těmito příznaky byly podélné praskliny v asfaltu a trhliny na rodinném domku č.p. 438, který se nalézá přímo na těle sesuvu. Hodnota přitížení silnice třetí třídy byla stanovena na 20 kPa a přitížení rodinného domku bylo stanoveno na 150 kPa. Tyto hodnoty nebyly vypočítány, nýbrž byly stanoveny odborníkem jako odpovídající hodnoty pro dané objekty. Pro tuto modelovou situaci jsou tyto hodnoty postačující.
12.3.2 Geometrie svahu
Geometrie svahu je zadávána v souřadnicovém systému X-Y (viz. Tab.12.3.2.1). Geometrií se rozumí zakreslení povrchu svahu, přičemž je nezbytné, aby byl tento obrazec uzavřen. Dále vykreslíme průběh geologických vrstev tvořících geologickou stavbu svahu.
Nutností pro výpočet napěťo-deformačního stavu je zadání geometrických okrajových podmínek zadaného svahu. Okrajovými podmínkami je tzv. „tuhá vana“, přičemž matematický model při aplikaci „tuhé vany“ je na vertikálních hranicích omezen proti horizontálnímu posunu a na spodní horizontální hranici omezen proti posunu ve směru horizontálním i směru vertikálním.
Tab. 12.3.2.1
Souřadnice bodů modelu vytvořeného v programovém systému PLAXIS 2D
|
Souřadnice bodů – PLAXIS |
||||||||
|
Bod č. |
X [m] |
Y [m] |
Bod č. |
X [m] |
Y [m] |
Bod č. |
X [m] |
Y [m] |
|
0 |
0 |
0 |
22 |
28,8 |
11,5 |
44 |
28,8 |
17 |
|
1 |
0 |
25 |
23 |
72,2 |
8 |
45 |
42,5 |
14,5 |
|
2 |
7,4 |
24,7 |
24 |
42,5 |
13,5 |
46 |
67,8 |
11,3 |
|
3 |
10,3 |
22,7 |
25 |
42,5 |
9,5 |
|
|
|
|
4 |
12,1 |
22,5 |
26 |
42,5 |
18 |
|
|
|
|
5 |
18 |
21,2 |
27 |
2,5 |
25 |
|
|
|
|
6 |
67,8 |
12 |
28 |
6,5 |
25 |
|
|
|
|
7 |
72,2 |
11 |
29 |
0 |
21,5 |
|
|
|
|
8 |
83,2 |
7 |
30 |
5 |
21 |
|
|
|
|
9 |
86,6 |
5,3 |
31 |
7,4 |
21 |
|
|
|
|
10 |
90 |
7 |
32 |
10,3 |
20,5 |
|
|
|
|
11 |
90 |
0 |
33 |
12,1 |
20 |
|
|
|
|
12 |
4,2 |
22 |
34 |
12,5 |
20 |
|
|
|
|
13 |
5,8 |
21,5 |
35 |
18 |
19,5 |
|
|
|
|
14 |
12,5 |
18 |
36 |
28,8 |
18,5 |
|
|
|
|
15 |
17,3 |
16,5 |
37 |
42,5 |
16 |
|
|
|
|
16 |
28,8 |
13,5 |
38 |
67,8 |
11,5 |
|
|
|
|
17 |
0 |
21,2 |
39 |
7,4 |
20,7 |
|
|
|
|
18 |
4,2 |
20,8 |
40 |
10,3 |
20 |
|
|
|
|
19 |
5,8 |
20,3 |
41 |
12,1 |
19,5 |
|
|
|
|
20 |
12,5 |
16 |
42 |
12,5 |
19,3 |
|
|
|
|
21 |
17,3 |
13,8 |
43 |
18 |
18 |
|
|
|
12.3.3 Geotechnické parametry
zemin a hornin
Mezi vstupní data, potřebná pro výpočet napěťo-deformačního stavu svahu, patří popisné, deformační a pevnostní charakteristiky zemin a hornin, tvořící geologický profil.
Stanovením
geometrie, s vykresleným průběhem geologických vrstev těla sesuvu, můžeme
přiřadit k vrstvám geotechnické parametry odpovídající zeminám a horninám
(viz. Tab. 12.3.3.1 a Tab. 12.3.3.2). Je nutno zadat takové vstupní
geotechnické vlastnosti zjištěných hornin a zemin, aby byl při modelování co
nejvěrohodněji zachycen reálný napěťo-deformační stav, jenž je na skutečném sesuvu.
Tab. 12.3.3.1 Geotechnické
parametry hornin použité v modelech s vysokou hladinou podzemní vody
|
Typ
horniny |
ČSN 73 1001 |
Konzistence |
jef (°) |
gn(kN/m3) |
cef (kPa) |
n ( - ) |
Ed (MPa) |
K (m .
s-1) |
|
(zvětrání) |
||||||||
|
jíly |
F4
|
tuhá |
22 |
18,5 |
37 |
0,35 |
11 |
1 . 10-4 |
|
písky |
S5 |
- |
18 |
18 |
4 |
0,35 |
12 |
0,1 |
|
prachovec |
R5-R6 |
zvětralý |
25 |
20 |
80 |
0,13 |
44,9 |
1 . 10-8 |
Tab. 12.3.3.2 Geotechnické
parametry hornin použité v modelech s nízkou hladinou podzemní vody
|
Typ
horniny |
ČSN 73 1001 |
Konzistence |
jef (°) |
gn(kN/m3) |
cef (kPa) |
n ( - ) |
Ed (MPa) |
K (m .
s-1) |
|
(zvětrání) |
||||||||
|
jíly |
F4
|
tuhá |
27 |
18,5 |
44 |
0,35 |
11 |
1 . 10-4 |
|
písky |
S5 |
- |
18 |
18 |
4 |
0,3 |
12 |
0,1 |
|
prachovec |
R5-R6 |
zvětralý |
25 |
20 |
80 |
0,13 |
44,9 |
1 . 10-8 |
12.3.4 Voda ve výpočtu
Programem
PLAXIS lze do výpočtu napěťo-deformačního stavu vnést vliv vody. Přítomnost
vody v geologickém prostředí způsobuje, kvalitativní změny
fyzikálně-mechanických vlastností geologických vrstev profilu. Přítomnost vody
ve svahu je bezesporu nutným aspektem vzniku svahových pohybů, a matematický
model by měl faktor vody co nejpřesněji postihnout. K sesuvu došlo
především z důvodů usmyknutí nadloží po smykové ploše, kterou tvoří
zvodnělé vrstvy měkkých až kašovitých zemin.
Podle již
zmiňovaných variant z kapitoly 12.1.2 bude proveden stabilitní výpočet,
přičemž výchozí bude stav v době aktivizace sesuvu v roce 1997. Zde
výška hladiny podzemní vody dosahovala maxima (Tab. 12.3.4.1), což se bezesporu
projevilo nízkou hodnotou stupně stability a výslednou nestabilitou svahu.
Tab. 12.3.4.1 Výška hladiny podzemní vody
Před sanací: Po sanaci:
|
Vrty |
HV-1 |
HV-2 |
HV-3 |
|
Výška hladiny p.v. [m] |
2,13 |
3,39 |
1,95 |
|
Vrty |
J2 |
J3 |
J4 |
|
Výška hladiny p.v.[m] |
1,9 |
0,55 |
0,8 |
12.3.5
Výsledky výpočtů programu PLAXIS
Pro vykreslení
geometrie svahu a přiřazení materiálových charakteristik geologickým vrstvám,
je nutno zakreslit průběh výšky hladiny podzemní vody tělesem svahu. Výstupem
je napěťo-deformační stav pro svah s původní hladinou podzemní vody a
napěťo-deformační stav, při zavedení sanačních opatření.
12.3.6
Výstupy programového systému
Modelováním výchozího stavu s maximální hladinou podzemní vody v tělese sesuvu bez účinků sanačních prací byly zjištěny celkové deformace svahu ujížděním po smykové ploše. Při realizaci sanačního opatření, které vedlo ke snížení hladiny podzemní vody došlo k zastavení posunu v oblasti smykové plochy.
12.3.6.1 Vypočtený stupeň stability
Důležitou
vstupní hodnotou, určující stabilitu sesuvu je součinitel stability. Program
PLAXIS umožňuje stanovit koeficient bezpečnosti (součinitel stability). Určení
součinitele stability je možné provést globálně pro celou zájmovou oblast, tj.
program na svém výstupu zobrazí součinitele stability, odpovídající kritické
smykové ploše, nebo umožňuje určení lokálního součinitele v námi zadaných
elementech. Lokální součinitel stability je vhodný pro posouzení stability
klíčového místa. Podle součinitele stability se dále navrhuje možné sanační a
stabilitní opatření. Zpětně po započtení vlivu sanačního opatření lze zjistit
následný stupeň stability a rozhodnout o míře účinnosti sanace.
Program definuje koeficient bezpečnosti jako poměr původní soudržnosti zeminy, respektive úhlu vnitřního tření, k soudržnosti či úhlu vnitřního tření na mezi porušení:
F = c/cr = tgj / tgjr
c … soudržnost původní (vstupní)
j … původní (vstupní) úhel vnitřního tření
cr … soudržnost na mezi porušení
jr … úhel vnitřního tření na mezi porušení
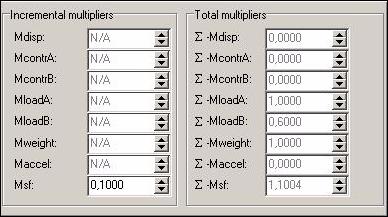
Obr. 12.3.6.1 a) Stupeň stability (F = 1,1004) před
započetím sanačních prací, s přitížením svahu rodinným domem a cestou
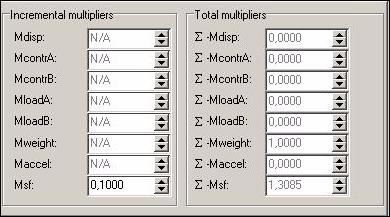
Obr. 12.3.6.1 b)
Stupeň stability (F = 1,3085) před započetím sanačních prací, bez přitížení
svahu rodinným domem a cestou třetí třídy
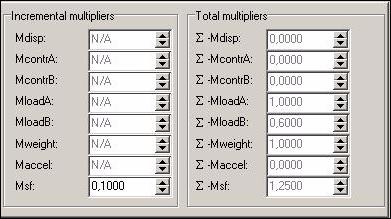
Obr. 12.3.6.1 c) Stupeň stability (F = 1,25) po
dokončení sanačních prací, s přitížením svahu rodinným domem a cestou třetí
třídy
Obr. 12.3.6.1 d) Stupeň
stability (F = 1,4868) po dokončení sanačních prací, bez přitížení svahu
rodinným domem a cestou třetí třídy
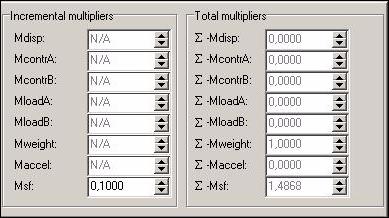
Modelováním a
výpočtem výchozího stavu po aktivaci sesuvu v roce 1997 byla zjištěna
hodnota součinitele stability 1,1004, přičemž hodnota součinitele stability pod
1,2 vypovídá o nestabilitě svahu, kde svah je ve stavu trvalého přetváření.
Zavedení sanačních opatření se projevilo ve stabilizačních výpočtech nárůstem součinitele stability na hodnotu 1,25. Pro takovou hodnotu součinitele stability je možno svah považovat za stabilní.
Varianty, kdy svah nebyl přitížen
rodinným domkem ani silnicí třetí třídy nám vykazují hodnoty součinitele
stability nad 1,3 , což vypovídá o zaručené dlouhodobé stabilitě svahu.
12.3.6.2 Smykové přetvoření
Grafické
výstupy se smykovým přetvořením svou povahou odpovídají výsledkům analýz
celkových deformací.
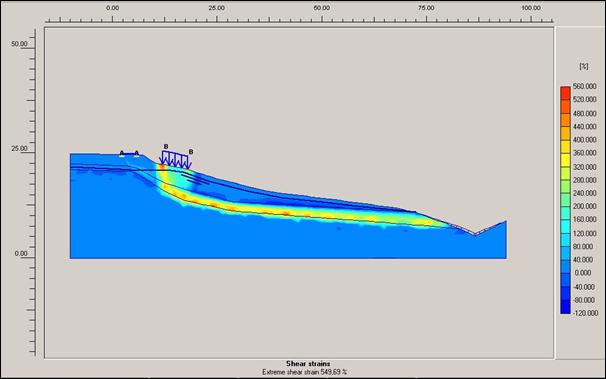
Obr.12.3.6.2a) Smykové přetvoření před započetím
sanačních prací, s přitížením svahu rodinným domem a cestou
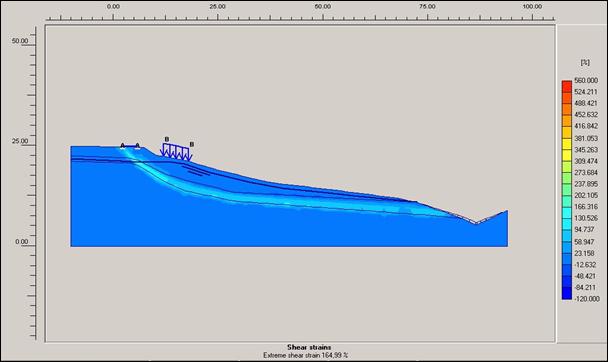
Obr.12.3.6.2b) Smykové
přetvoření před započetím sanačních prací, bez přitížení svahu rodinným domem a
cestou
Obr.12.3.6.2c) Smykové přetvoření po dokončení
sanačních prací, s přitížením svahu rodinným domem a cestou
Obr.12.3.6.2d) Smykové
přetvoření po dokončení sanačních prací, bez přitížení svahu rodinným domem a
cestou
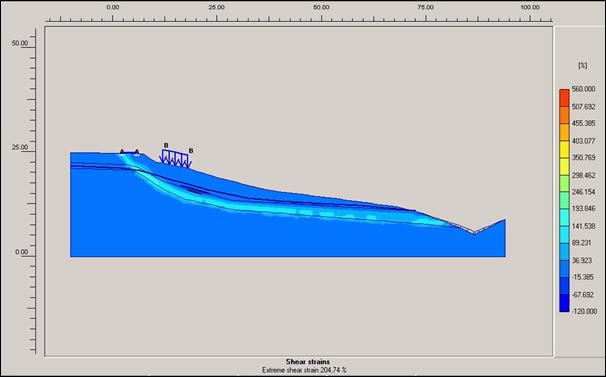
Kritická místa
tvoří plocha okolo vrstvy písku s jílem až jílovým pískem.
Z grafických výstupů lze odečíst, že k největšímu smykovému
přetvoření došlo před započetím sanačních prací. Přitížení rodinného domku lze
považovat za důležitý aspekt vzniku svahového přetvoření a to nejen ve variantě
před započetím sanačních prací, ale i po zavedení sanačních opatření.
12.3.6.3 Plastické body
V oblastech
smykových ploch, po kterých svahoviny ujíždějí, dochází ke zplastizování zemin,
což systém PLAXIS jednoznačně ve svém grafickém výstupu ukazuje. Na těchto
obrázcích lze vysledovat vznik tahových trhlin a místa plastického porušení.
Obr.12.3.6.3a) Plastické body před započetím sanačních prací, s
přitížením svahu rodinným domem a cestou
Obr.12.3.6.3b) Plastické body před
započetím sanačních prací, bez přitížení svahu rodinným domem a cestou
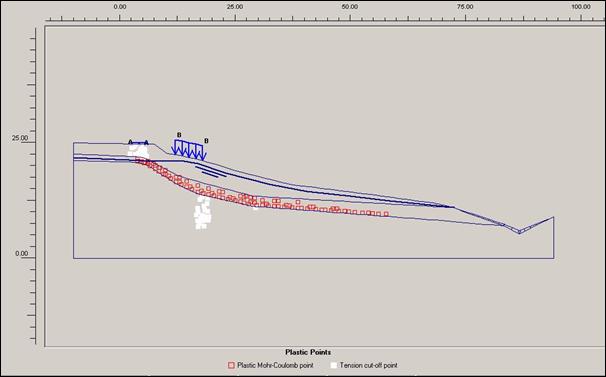
Obr.12.3.6.3c) Plastické body po dokončení sanačních prací, s přitížením
svahu rodinným domem a cestou
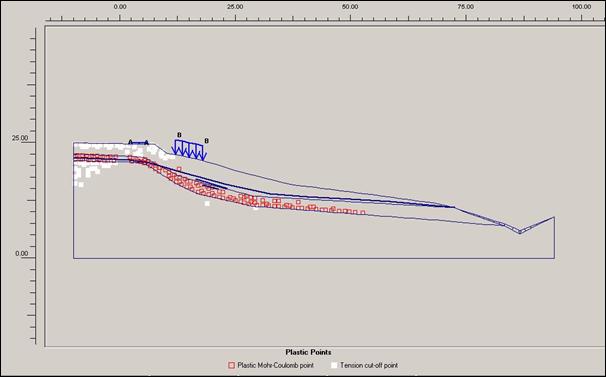
Obr.12.3.6.3d) Plastické body po dokončení sanačních
prací, bez přitížení svahu rodinným domem a cestou
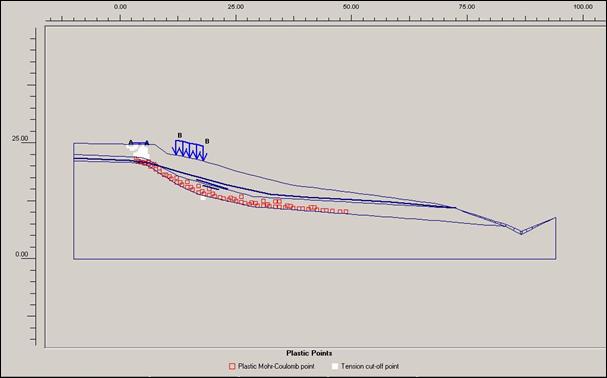
Jako výchozí
byl uvažován stav s maximální hladinou podzemní vody bez účinku sanačního
opatření. Zplastizované body prokázaly horizont, po kterém svahovina ujíždí. Ve
výstupu matematického modelu jsou také patrná místa odtrhů, jež svou lokalizací
odpovídají skutečným hranám, či prasklinám.
Díky sanačním
pracem došlo ke snížení počtu a rozmístění bodů zplastizování na bázi smykové
plochy.
12.3.6.4 Totální, horizontální a vertikální
posuny
Program PLAXIS
na těchto výstupech (Obr. 12.3.6.4 a až k) poukazuje na směr a délku celkového
posunu v určitých místech dané lokality.
Obr. 12.3.6.4 a) Totální posun před započetím
sanačních prací, s přitížením svahu rodinným domem a cestou
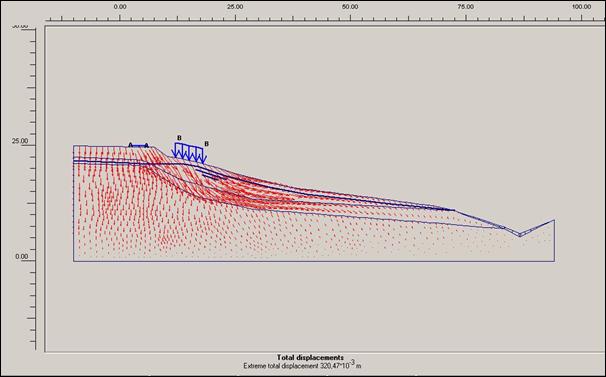
Obr.12.3.6.4 b) Totální posun před započetím sanačních
prací, bez přitížení svahu rodinným domem a cestou
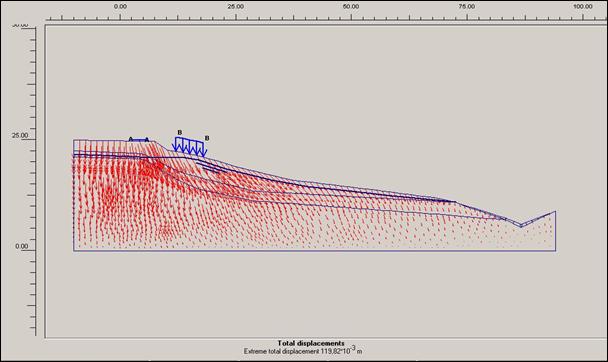
Obr.12.3.6.4 c) Totální posun po dokončení sanačních prací, s přitížením svahu rodinným domem a cestou
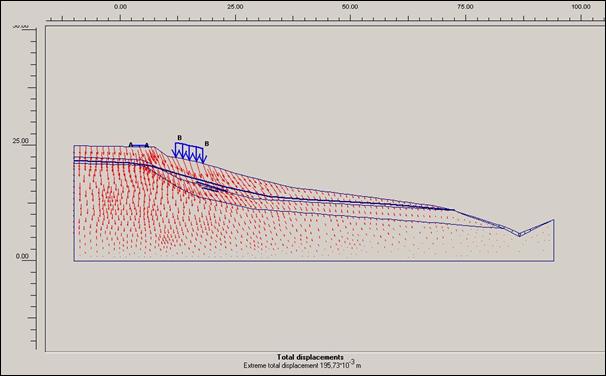
Obr.12.3.6.4 d) Totální posun po dokončení sanačních prací, bez přitížení svahu rodinným domem a cestou
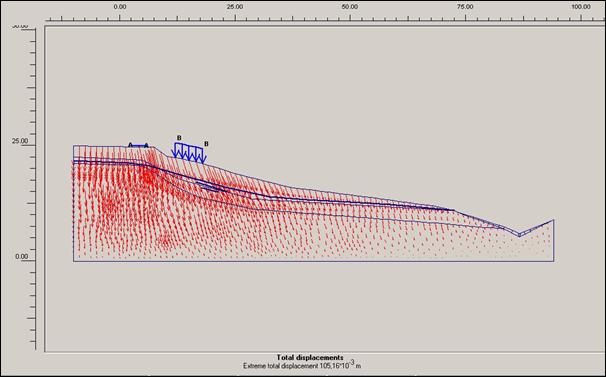
Obr.12.3.6.4 e) Horizontální posun před započetím sanačních
prací, s přitížením svahu rodinným domem a cestou
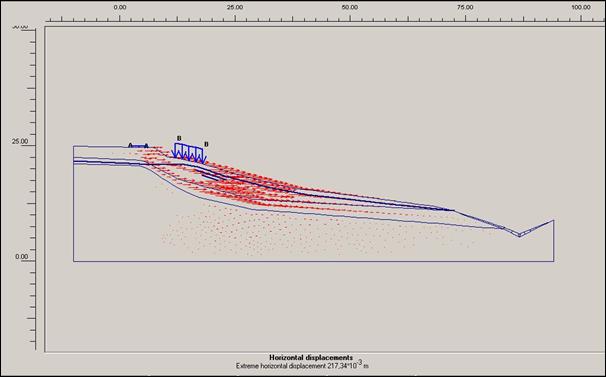
Obr.12.3.6.4 f) Horizontální posun před započetím sanačních
prací, bez přitížení svahu rodinným domem a cestou
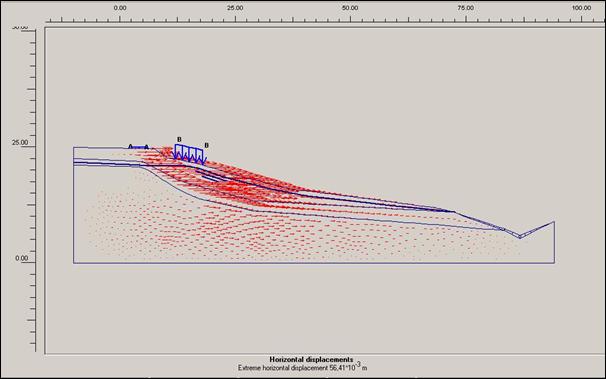
Obr.12.3.6.4 g) Horizontální posun po dokončení sanačních
prací, s přitížením svahu rodinným domem a cestou
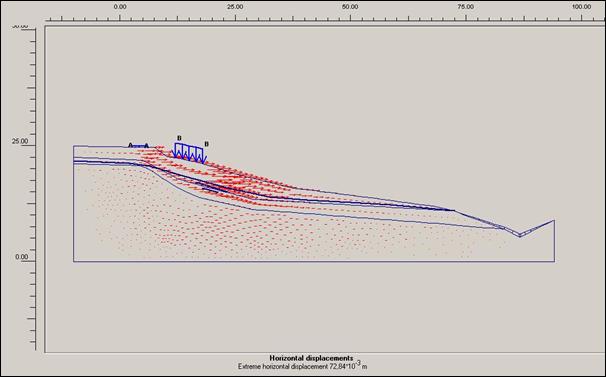
Obr.12.3.6.4 h) Horizontální posun po dokončení sanačních
prací, bez přitížení svahu rodinným domem a cestou
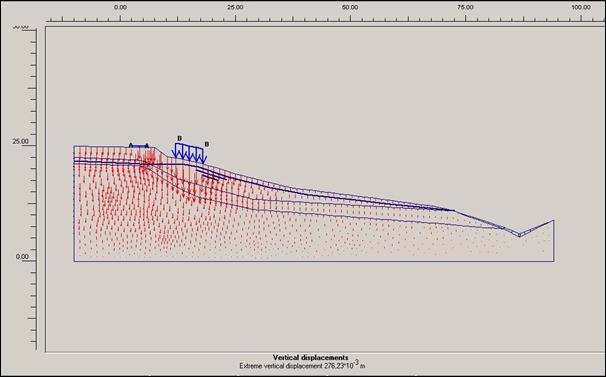
Obr.12.3.6.4 ch) Vertikální posun před započetím sanačních
prací, s přitížením svahu rodinným domem a cestou
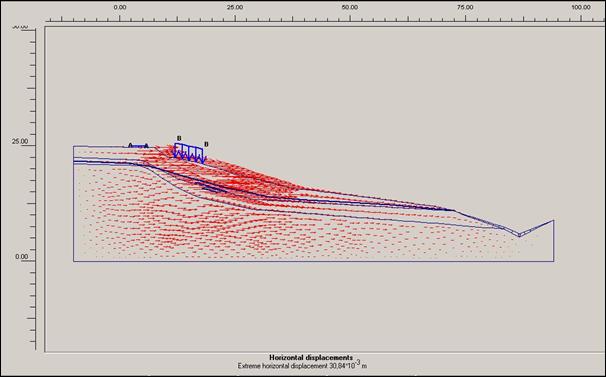
Obr.12.3.6.4 i) Horizontální posun před započetím sanačních
prací, bez přitížení svahu rodinným domem a cestou
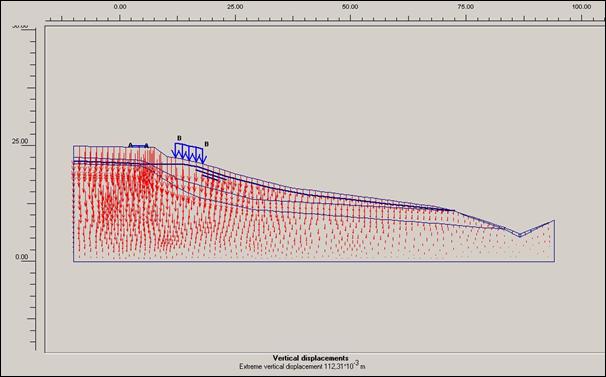
Obr.12.3.6.4 j) Vertikální posun po dokončení
sanačních prací, s přitížením svahu rodinným domem a cestou
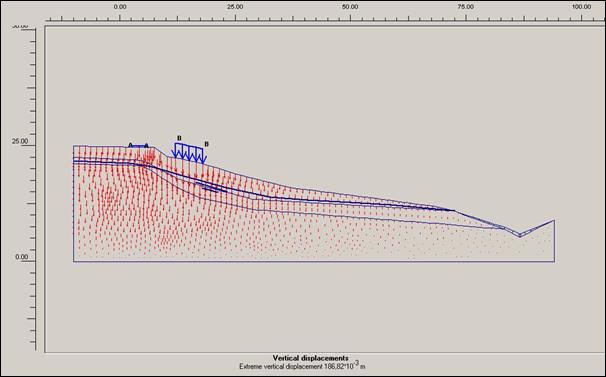
Obr.12.3.6.4 k) Vertikální posun po dokončení sanačních
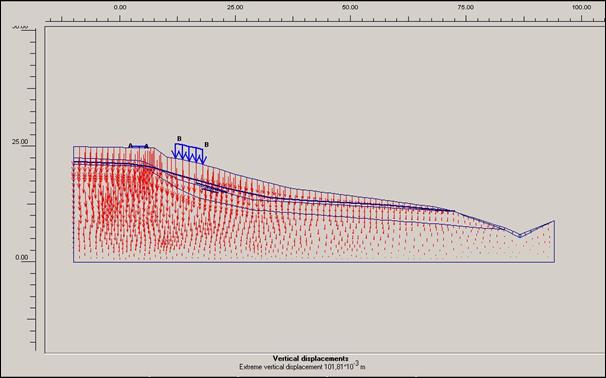
prací, bez přitížení svahu rodinným domem a cestou
Grafické
výstupy na obrázcích s přitížením jsou nositelem vyšších hodnot posunutí a
vyšší akumulace těchto posuvných sil než varianty bez přitížení rodinného domku
a vozovky třetí třídy.
12.3.6.5 Totální posuny v řezech pod
domkem a v patě svahu
Graficky jsou
zde znázorněny totální posuny na námi určených (lokálních) místech. Obrázky nám
znázorňují směr a sílu posunu v závislosti na hloubce.
Obr.12.3.6.5 a) Lokální posun
před započetím sanačních prací, s přitížením svahu rodinným domem a cestou pod
rodinným domkem
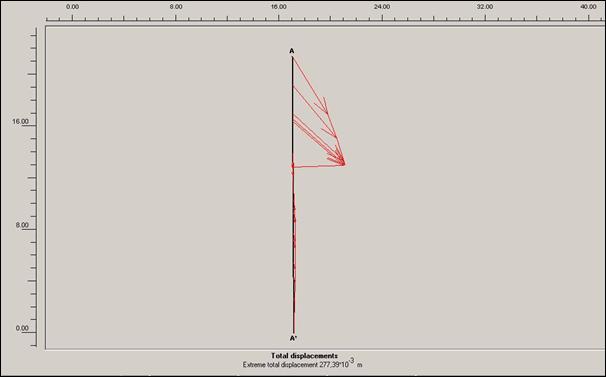
Obr.12.3.6.5 b)
Lokální posun před započetím sanačních prací, bez přitížení svahu rodinným
domem a cestou pod rodinným domkem
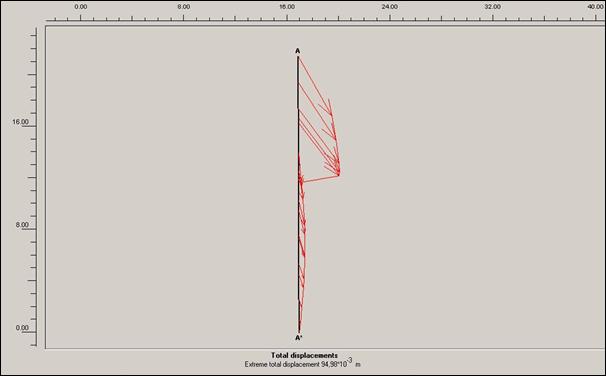
Obr.12.3.6.5 c)
Lokální posun po dokončení sanačních prací, s přitížením svahu rodinným domem a
cestou pod rodinným domkem
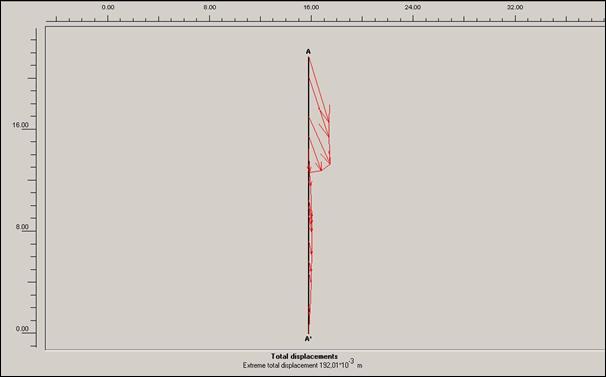
Obr.12.3.6.5 d)
Lokální posun po dokončení sanačních prací, bez přitížení svahu rodinným domem
a cestou pod rodinným domkem
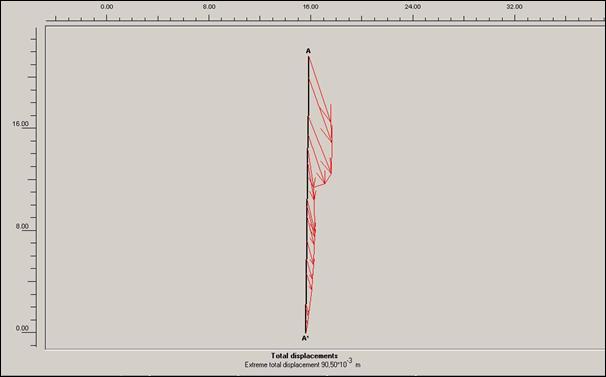
Obr.12.3.6.5 e) Lokální posun
před započetím sanačních prací, s přitížením svahu rodinným domem a cestou
v patě svahu
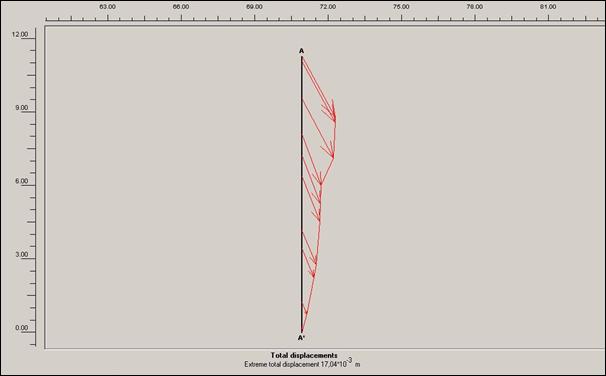
Obr.12.3.6.5 f)
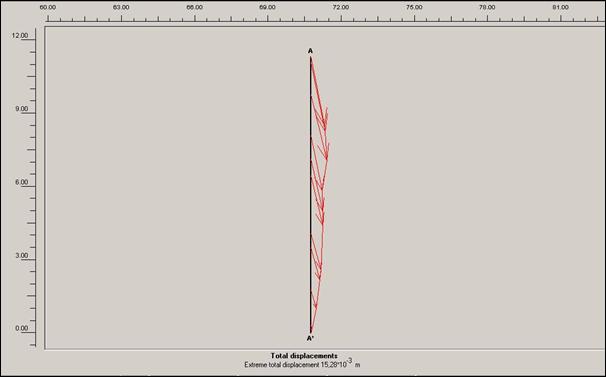
Lokální posun před započetím sanačních prací, bez přitížení svahu rodinným
domem a cestou v patě svahu
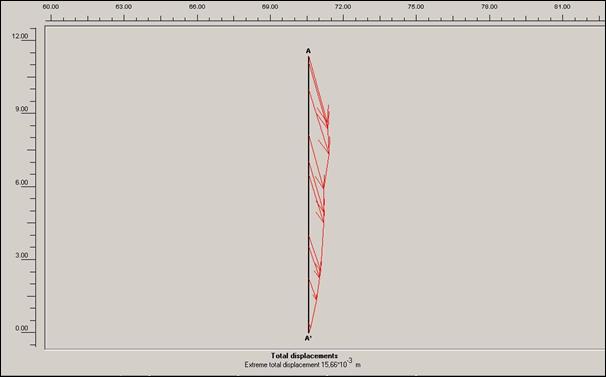
Obr.12.3.6.5 g)
Lokální posun po dokončení sanačních prací, s přitížením svahu rodinným domem a
cestou v patě svahu
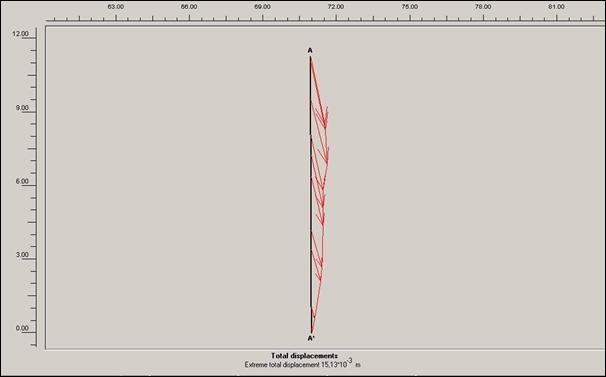
Obr.12.3.6.5 h) Lokální posun po dokončení sanačních prací,
bez přitížení svahu rodinným domem a cestou v patě svahu
S výsledků
grafických výstupů lze nejlépe vysledovat vliv přitížení rodinného domku na
dané prostředí. Varianty s tímto přitížením mají nejen vyšší hodnoty
totálního posunutí, ale i trochu jiný směr působící síly v těle sesuvu.
Směr těchto sil je téměř svislý (u totálních posunů modelovaných pod rodinným
domem).
12.3.6.6 Deformace modelové sítě svahu
Tyto výstupy
nám stanovují míru přetvoření svahu v důsledku námi zadaných parametrů.
Dochází zde k porovnání vstupních dat (zadaný řez) a vypočtených dat
(deformace sítě).
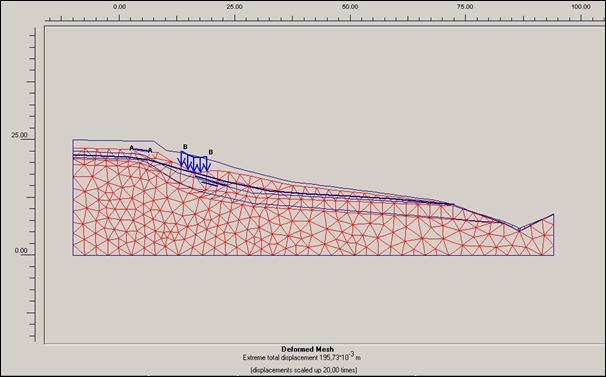
Obr. 12.3.6.6 a) Deformace sítě před započetím
sanačních prací, s přitížením svahu rodinným domem a cestou
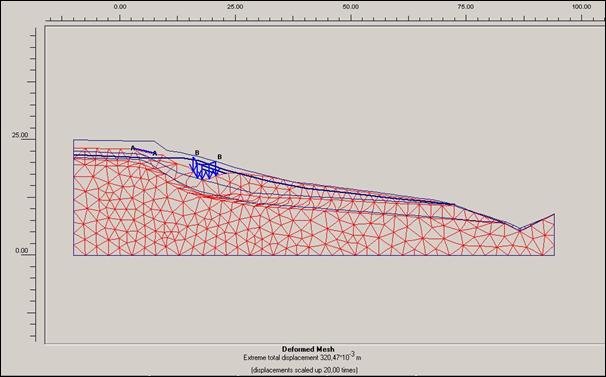
Obr. 12.3.6.6 b) Deformace sítě před započetím sanačních
prací, bez přitížení svahu rodinným domem a cestou
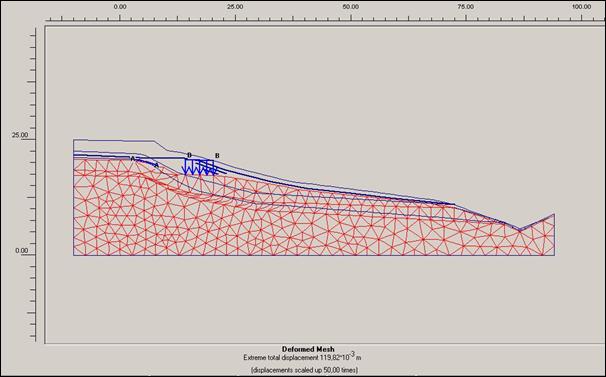
Obr. 12.3.6.6 c) Deformace sítě po dokončení sanačních prací, s
přitížením svahu rodinným domem a cestou
Obr. 12.3.6.6 d) Deformace sítě po dokončení sanačních
prací, bez přitížení svahu rodinným domem a cestou
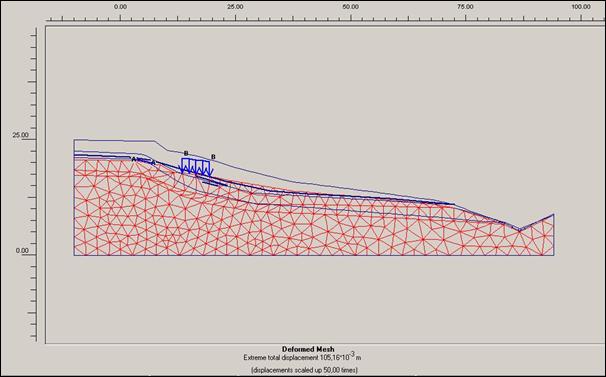
Deformace
zadané sítě zobrazující body propočítané pro danou lokalitu je viditelně
ovlivněna nejen výškou hladiny podzemní vody , ale i možným přitížením svahů.
Modelové situace řešené programem PLAXIS nám ukazují, že sanační práce provedené na této lokalitě vedené ke snížení hladiny podzemní vody vykazují známky značného zlepšení stability svahu. Na tomto modelovém projektu jsme si ověřili, že i přitížení na těle sesuvu má nemalý vliv na stabilitu svahu a tudíž by se mělo s hodnotami přitížení počítat, jinak může dojít k chybám řešení sanací na lokalitách.
12.4 GeoStar 3.3
12.4.1 Chrakteristika softwaru GeoStar
GeoStar 3.3 je
program pro výpočty stability svahů metodami mezní rovnováhy. Je zde řada
různých metod pro výpočty stability na rotačních i obecných smykových plochách.
Program dovoluje provádět výpočty jak s efektivními, tak i totálními
parametry smykové pevnosti.
Vstupní i výstupní data jsou řešena v souřadnicovém systému X-Y (viz.
Tab.12.4.1). Pro vypočtení profilu programu GeoStar platí pravidlo, že pata
svahu, tj. oblast s nejnižší vodorovnou souřadnicí se musí nalézat na levé
straně daného řezu. Výpočetní profil se skládá s jednotlivých vrstev. Ve
většině případů se vrstvou rozumí geometricky a materiálově určená část řezu
řešeným svahem, omezená polygonální hranicí. Po zadání geometrie vrstvy, ať
v grafickém, či dialogovém editoru se taktéž musí zadat geotechnické
parametry a informace o vlivu podzemní vody.
Tab. 12.4.1 Souřadnice vrstev
modelu vytvořeného v programovém systému GeoStar
|
vrstva 1 |
vrstva 2 |
vrstva 3 |
hl. podz. vody před sanací |
hl. podz. vody po sanací |
|||||
|
x |
y |
x |
y |
x |
y |
x |
y |
x |
y |
|
0 |
9 |
23 |
11 |
6,8 |
6 |
18 |
11 |
18 |
11 |
|
4 |
5,3 |
47 |
12 |
18 |
6,5 |
23 |
12 |
23 |
11,5 |
|
6,8 |
7 |
67,5 |
15,5 |
23 |
7 |
47 |
16 |
47 |
13,5 |
|
18 |
10,5 |
80 |
20 |
47 |
9 |
67,5 |
19 |
67,5 |
17 |
|
23 |
11,5 |
83 |
22 |
67,5 |
12,5 |
80 |
20,5 |
80 |
20 |
|
47 |
17 |
90 |
22,5 |
80 |
18 |
83 |
21 |
83 |
21 |
|
67,5 |
200 |
|
|
83 |
20 |
90 |
21,5 |
90 |
21,5 |
|
80 |
23 |
|
|
90 |
21,3 |
|
|
|
|
|
83 |
25 |
|
|
|
|
|
|
|
|
|
90 |
25 |
|
|
|
|
|
|
|
|