7. Modelování stability svahů

Metody matematického modelování stability svahových těles lze v zásadě rozdělit do dvou skupin:

I) metody mezní rovnováhy

II) numerické metody modelování stability

Každá z těchto metod má své výhody a nevýhody, z hlediska aplikačního se liší v možnostech zahrnutí různých reálných faktorů do výpočtu, v požadavcích na zjednodušení modelové situace, v časové náročnosti přípravy modelu a modelového výpočtu a rovněž v požadavcích na vstupní data výpočtu. Výstižnost matematického modelu a výsledky získané modelovým výpočtem je nutno vždy podrobit pečlivému rozboru.

7.1 Metody mezní rovnováhy

Základním principem metod mezní rovnováhy je řešení silové resp. momentové rovnováhy svahového tělesa nad zvolenou smykovou plochou. Jsou odvozeny za předpokladu existence takového stavu napjatosti prostředí, při němž je v celé zasažené oblasti mobilizována využitelná smyková pevnost zeminy a hledá se taková plocha, po níž by nejsnáze mohlo dojít k usmýknutí (kritická smyková plocha). Metody mezní rovnováhy nezohledňují přetvárné parametry horninového prostředí. Výsledkem řešení je stupeň stability, udávající podíl mezi pasivními silami (síly přispívající ke stabilitě svahu) a silami aktivními (síly přispívající k nestabilitě svahu), metody neumožňují získat informaci o průběhu napětí a deformací ve svahovém tělese. Smykové plochy mohou mít v závislosti na typu zeminy různý tvar (rovinný u nesoudržných zemin; zakřivený, nejčastěji kruhový, u soudržných zemin). Z řady metod mezní rovnováhy jsou pro řešení stability svahového tělesa ze soudržných zemin nejčastěji používány proužkové (švédské) metody (např. Pettersonova a Bishopova metoda). V případě nejjednodušší Pettersonovy proužkové metody se celé těleso nad uvažovanou smykovou plochou rozdělí na určitý počet proužků, provede se vyhodnocení aktivních a pasivních sil odpovídajících tíhám jednotlivých proužků a vliv všech uvažovaných proužků se superponuje (Hrubešová, 2003).

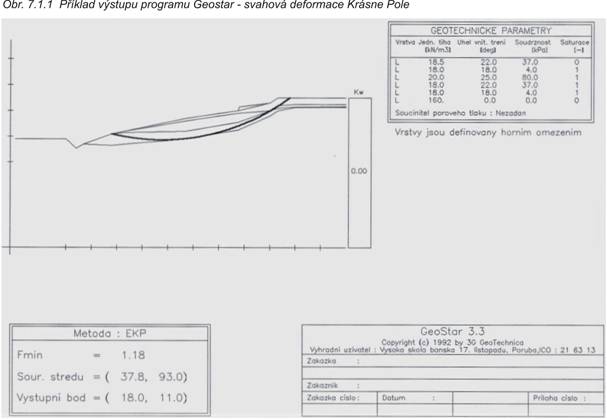
Metoda je implementována např. v programovém systému GEOSTAR (příklad výstupu obr. 7.1.1) a GEO4 (Česká republika) a GALENA (Austrálie).

7.2 Numerické metody modelování stability

Obecným principem všech numerických metod modelování je převedení úlohy pro řešení soustav diferenciálních rovnic (diferenciální rovnice rovnováhy, Lévyho rovnice souvislosti přetvoření apod.) na formálně jednodušší úlohu pro řešení soustavy lineárních algebraických rovnic pro neznámé hodnoty posunů resp. rychlostí posunů v uzlových bodech sítě. Na rozdíl od metod mezní rovnováhy nevyžadují zadání výchozí smykové plochy, zahrnují ve výpočtu i vliv přetvárného chování horninového prostředí, mají široké možnosti modelování geometrické a materiálové variability, umožňují získat komplexní představu o napěťodeformační a stabilitní situaci ve svahovém tělese a modelovat i případná sanační opatření. Jistou nevýhodou všech numerických metod je poněkud časově náročnější příprava výpočetního modelu, větší nároky na spolehlivost vstupních parametrů, delší doba výpočtu a v neposlední řadě i větší nároky na výpočetní techniku (nutnost řešení rozsáhlých soustav rovnic). Mezi nejčastěji používané numerické metody patří:

a) metoda konečných prvků (FEM)

b) metoda hraničních prvků (hraničních integrálů)(BEM)

c) metoda konečných diferencí (metoda sítí) (FDM)

d) metoda oddělených elementů (DEM)

Metody a) až c) jsou vhodné pro modelování úloh z oblasti kontinua, metoda oddělených elementů pak umožňuje řešit úlohy z oblasti diskontinua (Hrubešová, 2003).

7.2.1 Metoda konečných prvků

Metoda konečných prvků je numerická metoda , která je nejčastěji používána pro modelování rovinných i prostorových úloh mechaniky zemních těles. Patří mezi metody variační, vycházející z minimalizace energetického potenciálu. Podstatou metody je diskretizace zkoumané oblasti na rovinné nebo prostorové prvky konečných rozměrů (tzv. generace sítě), které jsou mezi sebou spojeny pouze konečným počtem uzlových bodů. Nejčastěji používaným typem konečných prvků v rovině jsou trojúhelníky. Zkoumané těleso je pak zatíženo silami působícími ve vrcholech (uzlech) konečných prvků, které jsou ekvivaletní původnímu zatížení. Na každém konečném prvku se volí vhodná aproximační funkce přesného řešení, která jednoznačně definuje stav posunutí uvnitř tohoto prvku pomocí posunutí jeho uzlů. Na základě této aproximace se pak s využitím podmínek pro minimalizaci energetického potenciálu odvodí pro každý uzel rovnice rovnováhy , která je funkcí těchto neznámých posunutí v uzlových bodech sítě. Řešením takto získané soustavy algebraických rovnic, představujících podmínky rovnováhy ve všech uzlových bodech ,jsou hodnoty posunů v těchto uzlových bodech. Tyto posuny pak společně s přetvárnými charakteristikami materiálu a zvoleným konstitutivním vztahem mezi napětím a přetvořením definují napěťový stav jak uvnitř prvku, tak i na jeho hranicích. Metoda konečných prvků umožňuje řešit úlohy se složitými okrajovými podmínkami, se složitou geometrií, umožňuje zohlednit chování materiálů charakterizované různými konstitučními vztahy, přičemž každý prvek může mít odlišné vlastnosti.

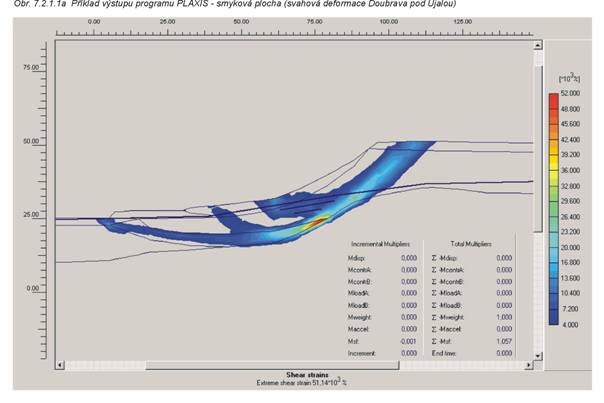
Metoda je implementována např. v programech PLAXIS (příklad výstupu obr.7.2.1.1a, obr. 7.2.1.1b, obr. 7.2.1.1c s geologickým profilem obr. 7.2.1.1d a geotechnickými parametry tab. 7.2.1.1) - Holandsko, CESAR-LCPC (Francie), GEO-SLOPE (Kanada).

7.2.2 Metoda hraničních prvků

Metoda hraničních prvků se začala rozvíjet především v souvislosti s potřebou snížit dimenzi výsledné soustavy rovnic, která byla výsledkem aplikace metody konečných prvků , a to především v případě prostorových modelů. Hlavní výhodou této metody je totiž snížení dimenze úlohy o jedničku, neboť se diskretizuje nikoliv celá uvažovaná oblast, ale pouze její hranice. Na každém hraničním prvku se aproximuje přesné řešení úlohy z uzlových bodů pomocí interpolačních funkcí. Po vyřešení odpovídající soustavy rovnic pro neznámé hodnoty posunů na hranicích oblasti se odpovídající hodnoty posunů resp. napětí uvnitř oblasti stanoví analyticky na základě tzv. fundamentálního řešení. Nevýhodami této metody je především nutnost znalosti fundamentálního řešení a dále nutný předpoklad homogenního prostředí uvnitř modelované oblasti. V  souvislosti s rozvojem stále výkonnější výpočetní techniky se tato metoda dostává poněkud do pozadí (Hrubešová, 2003).

7.2.3 Metoda konečných diferencí (metoda sítí)

Podstatou metody konečných diferencí je pokrytí oblasti, v níž hledáme řešení diferenciální rovnice, sítí, která se skládá z konečného počtu uzlových bodů. V každém bodě sítě se nahradí derivace v těchto uzlových bodech příslušnými diferencemi, tj. lineárními kombinacemi funkčních hodnot v okolních bodech. V závislosti na tom, zda volíme diference dopředné či zpětné, dostáváme různé typy metody sítí (metody explicitní, implicitní). Po záměně derivací diferencemi ve všech uzlových bodech dostáváme soustavu lineárních algebraických rovnic s neznámými hodnotami posunů v těchto uzlových bodech (Hrubešová, 2003).

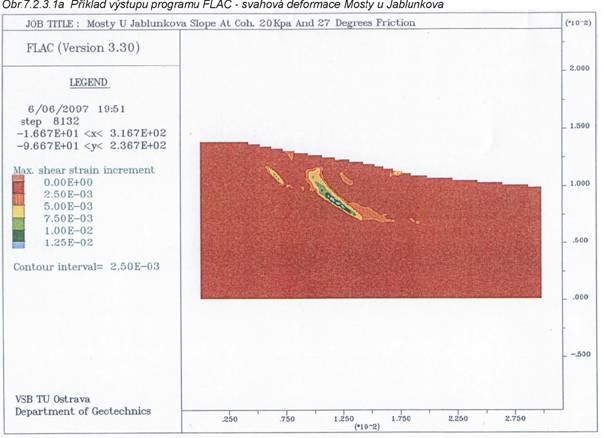
Metoda je implementována např. v programovém systému FLAC (příklad výstupu obr.7.2.3.1a, obr.7.2.3.1b) - ITASCA, USA.

7.2.4 Metoda oddělených elementů

Metoda oddělených elementů je metoda vhodná pro modelování diskontinua . Modeluje se vzájemná interakce tuhých nebo deformovatelných bloků, přičemž úloha diskontinuit je dominantní. Deformovatelné bloky se dále dělí na trojúhelníkové zóny , přičemž je pro výpočet přetvoření, napětí a vnitřních sil na základě hodnot rychlostí v uzlech zón využita modifikovaná explicitní metoda konečných diferencí. Úloha o spolupůsobení bloku se svým okolím je výpočetně řešena pro tak krátký časový okamžik, že impuls od jednoho bloku může být v daném výpočetním kroku předán pouze na jeho kontakty. Interakci a pohyb sousedících bloků lze pak popsat explicitními rovnicemi a šíření impulsů vyjádřit velkým počtem výpočetních cyklů, v nichž dochází k postupnému vyrovnávání nerovnovážného stavu bloků a kontaktů (dynamická relaxace) .Ve výpočetním cyklu se tedy řeší dynamická rovnováha a primárně neznámými hodnotami jsou hodnoty rychlostí v uzlech zón.

Tento algoritmus umožňuje modelovat statické a dynamické úlohy pro nespojité prostředí bloků a kontaktů s respektováním fyzikální nelinearity , plastického tečení a porušení látek včetně velkých deformací, smykání a separace bloků, modelování proudění kapalin v puklinách a řešení sdružené mechanicko-hydraulické popř. mechanicko-termální úlohy (Hrubešová, 2003).

Metoda je implementována v programovém systému UDEC (ITASCA, USA).