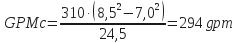Example No. 1: Capacity, Volumes and Strokes
Capacity of Drill Pipe, Heavy Weight Drill Pipe (HWDP), Casing or Open Hole in bbl/ft
Di = inside diameter (ID) if drill pipe, HWDP, drill collars, casing or open holes in inches.
Capacity of Casing or Open Hole between Drill Pipe, HWDP or Casing in bbl/ft
Dh = inside diameter of casing or open hole in inches,
Dp = outside diameter (OD) of drill pipe, HWDP or casing in inches.
Capacity of Drill Pipe, HWDP, Casing or Open Hole in ft/bbl
Capacity of Casing or Open Hole between Drill Pipe, HWDP or Casing in ft/bbl
Volume of Drill Pipe, HWDP, Drill Collar or Casing in bbl
Lp = length of drill pipe, HWDP, drill collars or casing in ft.
Volume between Drill Pipe, HWDP or Casing and the Casing or Open Hole in bbl
Lp = length of drill pipe, HWDP, drill collars, open hole or casing in ft.
♦ Rule of Thumb: Hole Volume
Example: Determine volumes and strokes for following:
| Item | Size, Inches | Weight per foot | Length, Feet |
|---|---|---|---|
| Riser | 18 ¾ (ID) | 5075 | |
| Intermediate Casing | 13 5/8 x 12 ¼ | 88,2 | 8425 |
| Open Hole | 9 7/8 | 4000 |
| Item | Size, Inches | Weight per foot | Length, Feet |
|---|---|---|---|
| DP | 6 5/8 x 5,965 | 25,2 | 15900 |
| HWDP | 6 5/8 x 4 ½ | 63,2 | 1000 |
| DC | 8 ½ x 2 13/16 | 172 | 600 |
| Item | Size, Inches | Efficiency, % | Output, bbl/stk | SPM |
|---|---|---|---|---|
| Hole Pumps | 5 ½ x 14 | 97 | 0,100 | 210 |
| Booster Pump | 6 x 6 | 97 | 0,051 | 180 |
Step 1: Calculate the drill string volume:
-
Drill Pipe Volume:
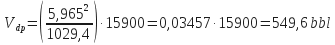
-
Heavy Weight Drill Pipe (HWDP) Volume:
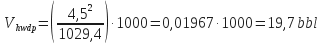
-
Drill Collars Volume:
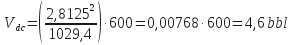
-
Total Drill String Volume:
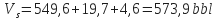
Step 2: Calculate the Annular Volume:
-
Drill Pipe/Riser Annular Volume:
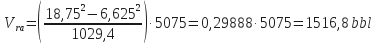
-
Drill Pipe/Casing Annular Volume:
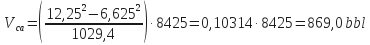
-
Open Hole/Drill Pipe Annular Volume:
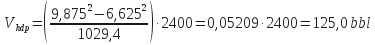
-
Open Hole/HWDP Annular Volume:
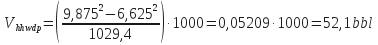
-
Open Hole/Drill Collars Annular Volume:
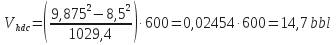
-
Total Annular Volume:
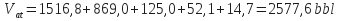
-
Total Volume of Hole System:
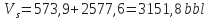
Example No. 2: Drill String Design (Limitations)
The following will be determined:
Length of bottom hole assembly (BHA) necessary for a desired weight on bit (WOB).
Feet of drill pipe that can be used with a specific bottom hole assembly.
Calculated the Length of BHA Necessary for Desired Weight on the Bit
Step 1: Calculate the Buoyancy Factor:
Ws = weight of steel in lbm/gal,
Wm = weight of mud or completion brine fluid (CBF) in lbm/gal.
Step 2: Calculate the Length of BHA Necessary for Desire Weight on the Bit
Wbit = desired weight on bit (WOB) in lb,
fdc = safety factor to place neutral point in drill collars,
Wdc = weight of drill collar in lb/ft.
Example: Calculate the BHA length necessary for desired WOB:
Safety factor
Mud weight
Drill collar weight (8 in. x 3 in.)
Weight of steel
= 15%
= 12,0 lbm/gal
= 147 lb/ft
= 65,5 lbm/gal
Step 1: Calculate the Buoyancy Factor:
Step 2: Calculate the Length of the BHA Necessary for this Weight on Bit:
Calculate the Feet of Drill Pipe that can be Used with a Special Bottom Hole Assembly (BHA)
Step 1: Calculate the Buoyancy Factor:
Step 2: Calculate the Maximum Length of Drill Pipe that can be Run into the Hole with a Specific BHA Assembly:
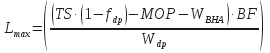
TS = tensile strength for new drill pipe in lb,
fdp = safety factor to correct new drill pipe to no. 2 pipe,
MOP = margin of overpull in lb,
WBHA = weight of the BHA in lb,
Wdp = weight of drill pipe with tool joint in lb/ft.
Step 3: Calculate the Total Depth that can be Reached with a Specific BHA in ft:
LBHA = length of BHA to be run in ft.
Example:
Tensile strength
BHA weight in air
BHA length
Desired overpull
Safety factor
= 881,040 lb
= 50000 lb
= 500 ft
100000 lb
= 10%
Result: DT = 26,013 ft
Example No. 3: Cementing Calculations
Cement Additive Calculations
Step 1: Calculate the Weight of Additive per Sack of cement in lb:
Va% = volume percent of additive for cement mixture,
94,0 = pounds of cement in one sack (sk).
Step 2: Total Water Requirement for each Sack of Cement in gal/sk:
Vcw = volume of water requirement for cement portion in gal/sk,
Vaw = volume of water requirement for additive portion in gal/sk.
Step 3: Calculate the Volume of the Cement Slurry in gal/sk:
SGcmt = specific gravity of dry cement,
SGa = specific gravity of dry additive,
8,33 = density of fresh water in lbm/gal.
Step 4: Calculate the Yield of the Cement Slurry in ft3/sk:
7,48 = volume of fresh water in gal/ft3.
Step 5: Calculate the Cement Slurry Density in lbm/gal:
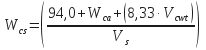
Example: using a Class A cement plus 4% bentonite with normal mixing water, calculate the following:
- Amount of bentonite to add in lb/sk,
- Total water volume requirement for the slurry in gal/sk,
- Slurry yield in ft3/sk,
- Slurry weight in lbm/gal.
Step 1: Calculate the Weight of the Bentonite Additive:
Step 2: Calculate the Total Water Requirement per Sack of Cement Used:
Step 3: Calculate the Total Volume of the Cement Slurry:
Step 4: Calculate the Yield of the Cement Slurry:
Step 5: Calculate the Cement Slurry Density:
Water Requirements
Step 1: Calculate the Weight of Cement Additive Materials in lb/sk:
Step 2: Calculate the Water Requirement for the Slurry using Material Balance Equation:
D1 V1 = D2 V2
V1 = volume of item 1 in consistent units,
D2 = density of item 2 in consistent units,
V2 = volume of item 2 in consistent units.
Example: Using a Class H cement plus 6% bentonite to be mixed at 14,0 lb/gal, calculate the following:
- Bentonite requirement in lb/sk,
- Water requirement in gal/sk,
- Slurry yield in ft3/sk,
- Check the slurry weight in lbm/gal.
Step 1: Calculate the Weight of Cement Additive Materials
Step 2: Calculate the Volume of Cement Slurry
Step 3: Calculate the Water Requirement using the Material Balance Equation
Step 4: Calculate the Yield of the Cement Slurry
Step 5: Recheck the Cement Slurry Density
RESULT: 14,0 lb/gal
Example No. 4: Pressure Requirement to Break Circulation
Pressure Requirement to Break the Mud´s Gel Strength inside the Drill String in psi
Step 1: Calculate the Pressure Requirement to Break the Mud´s Gel Strength inside the Drill String
τgs = 10 min gel strength of drilling fluid in lb/100 ft2,
Di = inside diameter of drill pipe in inches,
Lds = length of drill string in ft.
Step 2: Calculate the Pressure Required to Break the Mud´s Gel Strength in the Annulus:
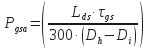
Dh = diameter of the annulus in inches.
Step 3: Calculate the Total Pressure Required to Break Circulation:
Example: Calculate the pressure required to break circulation in the well with this data:
Gel strength (10 or 30 minute) = 18 lb/100 ft2
Drill string = 6 5/8 x 5,965 in.
Hole size = 12 ¼ in.
Depth (MD) = 15000 ft
Step 1: Calculate the Pressure Required to Break the Mud´s Gel Strength inside the Drill String:
Step 2: Calculate the Pressure Required to Break the Mud´s Gel Strength in the Annulus:
Step 3: Calculate the Total Pressure Required to Break Circulation:
Calculate the Effective Gel Strength Based on the Actual Pressure Required to
Break the Circulation
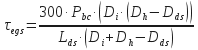
Pbc = actual pressure required to break circulation in the well in psi.
Example: Calculate the effective gel strength with the following data:
Pressure required to break circulation = 475 psi
Drill string length = 15000 ft
Hole size = 12 ¼ in.
Drill string size = 6 5/8 x 5,965 in.
RESULT: τegs = 27,5 lb/100 ft2
Example No. 5: Drilling Fluids - I
Increase Mud Density with No Base Liquid Added and No Volume Limit
- Short formula for mud weight increase:
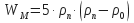 where:WM = number of 100 lb sacks of weight material required for 100 bbls of mud,
where:WM = number of 100 lb sacks of weight material required for 100 bbls of mud,
ρ0 = original mud weight in ppg,
ρn = new mud weight in ppg. -
Volume increase based on the amount of weight material
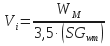 where:Vi = volume increase in bbls,
where:Vi = volume increase in bbls,
SGwm = specific gravity of weight material.Examples: Calculate the number of sacks of 4,2 ASG of barite required to increase the density of 100 bbls of 12,0 ppg (ρ0) mud to 14,0 ppg (ρn) and the resultant volume increase:
WM = 5·14,0·(14,0-12,0)
WM = 140 sacks of barite required for 100 bbls of 12,0 ppg mud
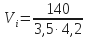
Vi = 9,5 bbls volume increase
- Increase mud weight:
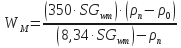 where:350 = weight of 1 barrel of fresh water in lbs,
where:350 = weight of 1 barrel of fresh water in lbs,
8,34 = mud weight of fresh water in lb/gal (ppg),
SGwm = specific gravity of weight material, gm/cc. - Volume increase with 100 lb sacks of weight material based on the change in mud weight:
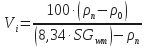 where:Vi = volume increase in bbls.
where:Vi = volume increase in bbls.Example: Calculate the number of sacks of 4,2 ASG barite required to increase the density of 100 barrels of 12,0 ppg (ρ0) mud to 14,0 ppg (ρn):
RESULT: Vi = 9,5 bbls volume increase
Example No. 6: Drilling Fluids - II
Mud Weight Reduction with Base Liquid
Example: Determine the number of barrels of fresh water weighing 8,34 ppg required to reduce the mud weight of 100 bbls of water – base mud (WBM) from 14,0 ppg to 12,0 ppg:
Example: Determine the number of barrels of base oil weighing 6,7 ppg required to reduce the mud weight of 100 bbls of synthetic – base mud (SBM) from 14,0 ppg to 12,0 ppg:
RESULT: Va = 37,7 bbls of oil are required
Mixing Fluids of Different Densities (The Material Balance Formula)
where: Vf = final volume in bbls, gals, etc.,
ρf = final mud weight in ppg, lb/ft3, etc.,
V1 = volume of fluid 1 in bbls, gals, etc.,
Ρ1 = mud weight of fluid 1 in ppg, lb/ft3, etc.,
V2 = volume of fluid 2 in bbls, gals, etc.,
Ρ2= mud weight of fluid 2 in ppg, lb/ft3, etc.
Example: A limit is placed on the desired volume:
Determine the volume of 11,0 ppg mud and 14,0 ppg mud required to build 300 bbl of 11,5 ppg mud:
300 · 11,5 = ((300 – x) · 11,0) + 14,0 · x
3450 = (3300 – 11,0 x) + 14,0 · x
3450 – 3300 = 3,0 x
150 = 3,0 x
x = 50 bbls of 14,0 ppg mud
300 – 50 = 250 bbls of 11,0 ppg required
To check the volumes are corrected:
300 · 11,5 = 250 · 11,0 + 50 · 14,0
3450 = 2750 + 700
3450 = 3450
To check the final mud weight:
300 x = 250 · 11,0 + 50 · 14,0
300 x = 2750 + 700
x = 3450/300 = 11,5 ppg
Example: No limit is placed on volume:
Determine the final mud weight when the following two muds are mixed together:
Given: 400 bbl of 11,0 ppg mud and 400 bbl of 14,0 mud
RESULT: ρf = 12,5 ppg
Example No. 7: Drilling Fluids - III
Solid Analysis
NOTE: Steps 1 – 4 are performed on high salt content muds. For low – chloride muds, begin with Step 5.
Step 1: Calculate the Volume of Salt water in Percent (%):
Cl = chloride content measured from the filtrate in ppm,
W% = volume of water in mud from the retort in %.
Step 2: Calculate the Volume of the Suspended Solids in Percent (%):
O% = oil content in %.
Step 3: Calculate the Average Specific Gravity (ASG) of the Salt Water:
Step 4: Calculate the Average Specific Gravity of the Solids Suspended in the Mud:
O% = volume of oil in the mud in %,
OASG = specific gravity of base oil being used in mud (0,84 for diesel; 0,80 for IO).
Step 5: Calculate the Average Specific Gravity of Solids without Salt in Water Phase:
Step 6: Calculate the Volume of Low Gravity Solids (LSG) in percent (%):
Step 7: Calculate the Amount of LGS in lb/bbl:
Step 8: Calculate the Volume of the Weight Material in Percent (%):
Step 9: Calculate the Amount of High Specific Gravity Weight Material in Pounds (lbs):
Step 10: Calculate the Amount of Bentonite (High – quality LGS) in the Mud:
-
If the cation exchange capacity (CEC) of the formation clays and the methylene blue test (MBT) of the mud are know:
- Calculate the Amount of Bentonite in the Mud in lb/bbl:
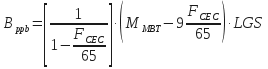 where:Bppb = amount of bentonite in the mud in lb/bbl,
where:Bppb = amount of bentonite in the mud in lb/bbl,
FCEC = CEC of the formation solids,
MMBT = MBT of the mud. - Calculate the Volume of Bentonite in the Mud in Percent (%):
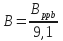 where:B% = amount of bentonite in the mud in %.
where:B% = amount of bentonite in the mud in %.
- Calculate the Amount of Bentonite in the Mud in lb/bbl:
- If the cation exchange capacities (CEC) of the formation clays are not know:
- Calculate the Volume of Bentonite in Percent (%):
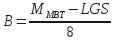
- Calculate the Amount of Bentonite in the Mud in lb/bbl:
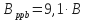
- Calculate the Volume of Bentonite in Percent (%):
Step 11: Calculate the Volume of Drill Solids in Percent (%):
Step 12: Calculate the Amount of Drill Solids in the Mud in lb/bbl:
Example:
Chlorides
MBT of mud
CEC of shale
= 73000 ppm
= 30 lb/bbl
= 7 lb/bbl
Oil
Solids
= 7,5% by volume (0,84 ASG diesel oil)
= 35,5% by volume (4,2 ASG barite)
Step 1: Calculate the volume of salt water in %:
Step 2: Calculate the volume of suspended solids in %:
Step 3: Calculate the average specific gravity (ASG) of the salt water:
Step 4: Calculate the average specific gravity of the solids suspended in the mud:
Step 5: Because a high chloride example is being used, Step 5 is omitted.
Step 6: Calculate the volume of low gravity solids (LGS) in percent (%):
Step 7: Calculate the amount of LGS in lb/bbl:
Step 8: Calculate the volume of the weight material in percent (%):
Step 9: Calculate the amount of high specific gravity weight material in pounds (lb/bbl):
Step 10: Calculate the amount of bentonite in the mud in lb/bbl:
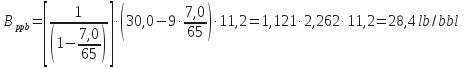
Step 11: Calculate the volume of bentonite in the mud in percent (%):
Step 12: Calculate the volume of drill solids in percent (%):
Step 13: Calculate the amount of drill solids in the mud in lb/bbl:
Example No. 8: Pressure Analyses
Gas Expansion Equations
Basic gas low:
P1V1 ÷ T1 = P2V2 ÷ T2
P2 = hydrostatic pressure at the surface or any depth in the wellbore, psi;
V1 = original pit gain, bbl;
V2 = gas volume at surface or at any depth if interest, bbl;
T1 = temperature of formation fluid, degrees Rankine (°R = °F + 460).
Basic gas law plus compressibility factor:
P1V1 ÷ T1Z1 = P2V2 ÷ T2Z2
Z2 = compressibility factor at the surface or at any depth of interest, dimensionless.
Shortened gas expansion equation:
P1V1 = P2V2
P2 = hydrostatic pressure plus atmospheric pressure (14,7 psi), psi;
V1 = original pit gain, bbl;
V2 = gas volume at surface or at any depth if interest, bbl.
Hydrostatic Pressure Exerted by Each Barrel of Mud in the Casing
- With pipe in the wellbore:
Example:
 Dh – 9 5/8 in. casing – 43,5 lb/ft
Dh – 9 5/8 in. casing – 43,5 lb/ft
Dp
Mud weight= 8,755 in. ID
= 5,0 in. OD
= 10,5 ppg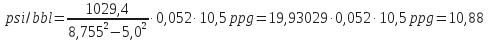
- With no pipe in the wellbore:
Example:
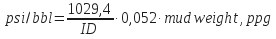 Dh – 9 5/8 in. casing – 43,5 lb/ft
Dh – 9 5/8 in. casing – 43,5 lb/ft
Mud weight= 8,755 in. ID
= 10,5 ppg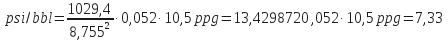
Surface Pressure during Drill Stem Tests
- Determine formation pressure from equation:
psi = formation pressure equivalent mud weight, ppg · 0,052 · TVD, ft - Determine oil hydrostatic pressure:
psi = oil specific gravity · 0,052 · TVD, ft - Determine surface pressure:
Surface pressure, psi = formation pressure, psi – oil hydrostatic pressure, psiExample: Oil bearing sand at 12500 ft with a formation pressure equivalent to 13,5 ppg. If the specific gravity of the oil is 0,5, what will be the static surface pressure during a drill stem test?
- Determine formation pressure, psi:
FT, psi = 13,5 ppg · 0,052 · 12500 ft = 8775 psi - Determine oil hydrostatic pressure:
psi = (0,5 · 8,33) · 0,052 · 12500 ft = 2707 - Determine surface pressure:
Surface pressure, psi = 8775 psi – 2707 psi = 6068 psi
Example No. 9: Bit Nozzle Selection – Optimized Hydraulics
These series of formulas will determine the correct jet sizes when optimizing for jet impact or hydraulic horsepower and optimum flow rate for two or three nozzles.
- Nozzle area, sq. in.:
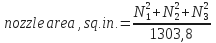
- Bit nozzle pressure los, psi (Pb):
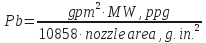
- Total pressure losses except bit nozzle pressure loss, psi (Pc):
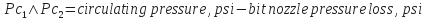
- Determine slope of line M:
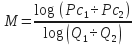
- Optimum pressure losses (Popt):
- For impact force:
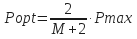
- For hydraulic horsepower:
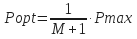
- For impact force:
- For optimum flow rate (Qopt):
- For impact force:
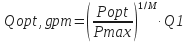
- For hydraulic horsepower:
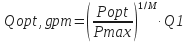
- For impact force:
- To determine pressure at the bit (Pb):
Pb = Pmax – Popt
- To determine nozzle area, sq. in.:
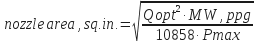
- To determine nozzles, 1/32 in, for three nozzles:
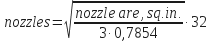
- To determine nozzles, 1/32 in. for two nozzles:
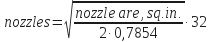
Example: Optimize bit hydraulics on a well with the following:
Select the proper jet size for impact force and hydraulic horsepower for 2 and 3 jets:
Jet sizes
Maximum surface pressure
Pump pressure 1
Pump rate 1
Pump pressure 2
Pump rate 2
= 17-17-17
= 3000 psi
= 3000 psi
= 420 gpm
= 1300 psi
= 275 gpm
- Nozzle area, sq. in.:

- Bit nozzle pressure loss, psi (Pb):
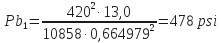
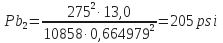
- Total pressure losses expect bit nozzle pressure loss (Pc), psi:
Pc1 = 3000 psi – 478 psi = 2522 psi
Pc2 = 1300 psi – 205 psi = 1095 psi
- Determine slope of line (M):
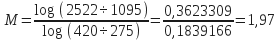
- Determine optimum pressure losses, psi (Popt):
- For impact force:
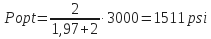
- For hydraulic horsepower:
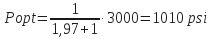
- For impact force:
- Determine optimum flow rate (Qopt):
- For impact force:
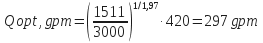
- For hydraulic horsepower:
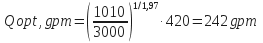
- For impact force:
- To determine pressure at the bit (Pb):
- For impact force:
Pb = 3000 psi –1511 psi = 1489 psi
- For hydraulic horsepower:
Pb = 3000 psi –1010 psi = 1990 psi
- For impact force:
- To determine nozzle area, sq. in.:
- For impact force:
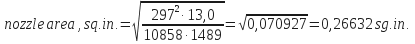
- For hydraulic horsepower:
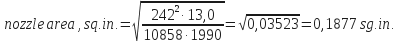
- For impact force:
- To determine nozzles, 1/32 in, for three nozzles:
- For impact force:
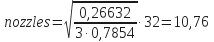
- For hydraulic horsepower:
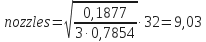
Note: usually the nozzles size will have a decimal fraction. The fraction times 3 will determine how many nozzles should be larger than that calculated.
- For impact force:
0,76 · 3 = 2,28 rounded to 2
so:1 jet
2 jets= 10/32
= 11/32 - For hydraulic horsepower:
0,03 · 3 = 0,09 rounded to 0
so:3 jets= 9/32 in.
- For impact force:
- To determine nozzles, 1/32 in. for two nozzles:
- For impact force:
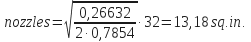
- For hydraulic horsepower:
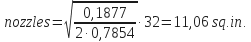
- For impact force:
Example No. 10: Critical Annular Velocity and Critical Flow Rate
- Determine n:
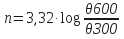
- Determine K:
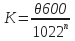
- Determine x:
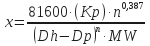
- Determine critical annular velocity:
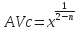
- Determine critical flow rate:
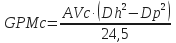
Nomenclature:
K
x
θ600
θ300
Dh
Dp
MW
AVc
GPMc
= dimensionless
= dimensionless
= 600 viscometer dial reading
= 300 viscometer dial reading
= hole diameter, in.
= pipe or collar OD, in.
= mud weight, ppg
= critical annular velocity, ft/min
= critical flow rate, gpm
Example:
Θ600
Θ300
Hole diameter
Pipe OD
= 64
= 37
= 8,5 in.
= 7,0 in.
- Determine n:
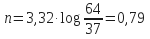
- Determine K:
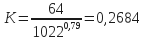
- Determine x:
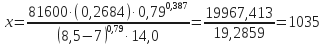
- Determine critical annular velocity:
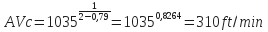
- Determine critical flow rate: